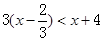将进货单价为30元的商品按40元出售时,每天卖出500件。据市场调查发现,如果这种商品每件涨价1元,其每天的销售量就减少10件。
(1)要使得每天能赚取8000元的利润,且尽量减少库存,售价应该定为多少?
(2)售价定为多少时,每天获得的利润最大?最大利润为多少?
在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
某校七年级社会实践小组去商场调查商品销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件, 并以每件120元的价格销售了400件.商场准备采取促销措施,将剩下的衬衫降价销售.请你帮商场计算一下,每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
已知:关于 的方程
的方程 。
。
(1)不解方程:判断方程根的情况;
(2)若方程有一个根为3,求 的值.
的值.
解不等式组
解不等式: