某校周四下午第五、六两节是选修课时间,现有甲、乙、丙、丁四位教师可开课。已知甲、乙教师各自最多可以开设两节课,丙、丁教师各自最多可以开设一节课.现要求第五、六两节课中每节课恰有两位教师开课(不必考虑教师所开课的班级和内容),则不同的开课方案共有( )种。
| A.20 | B.19 | C.16 | D.15 |
已知函数f(x)=ax2+2ax+4(a>0),若x1<x2 , x1+x2="0" , 则( )
| A.f(x1)<f(x2) | B.f(x1)=f(x2) | C.f(x1)>f(x2) | D.f(x1)与f(x2)的大小不能确定 |
设f(x)= 
 则不等式f(x)>2的解集为
则不等式f(x)>2的解集为
A.(1,2)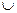 (3,+∞) (3,+∞) |
B.(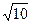 ,+∞) ,+∞) |
C.(1,2)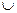 ( (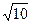 ,+∞) ,+∞) |
D.(1,2) |
若a>0,b>0,则不等式-b< <a等价于()
<a等价于()
A. <x<0或0<x< <x<0或0<x< |
B.- <x< <x< |
C.x<- 或x> 或x> |
D.x< 或x> 或x> |
不等式 的解集是()
的解集是()
A. |
B.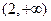 |
C.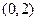 |
D.  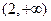 |
(山东文7)命题“对任意的 ”的否定是()
”的否定是()
A.不存在 |
B.存在 |
C.存在 |
D.对任意的 |