如图所示，轻质弹簧的劲度系数k＝20 N/cm，用其拉着一个重为200 N的物体在水平面上运动，当弹簧的伸长量为4 cm时，物体恰在水平面上做匀速直线运动，求：
(1)物体与水平面间的动摩擦因数．
(2)当弹簧的伸长量为6 cm时，物体受到的水平拉力多大？这时物体受到的摩擦力有多大？
(3)如果物体在运动的过程中突然撤去弹簧，而物体在水平面上能继续滑行，这时物体受到的摩擦力多大？
如图所示，水平传送带右端与竖直放置的光滑半圆形轨道在B点相切，半圆形轨道半径为R=0.4m。物块在与传送带等高的左侧平台上以4m/s的速度从A点滑上传送带。物块质量m=0.2kg，物块与传送带的动摩擦因数μ=0.4，g取10m/s2。
（1）若长度为2m的传送带以2m/s的速度绕顺时针匀速转动，求物块从A点到B点的时间；
（2）若传送带以5m/s的速度绕顺时针匀速度转动，且传送带足够长，求物块到达最高点C对轨道的压力。
（3）若传送带以5m/s的速度绕顺时针匀速度转动，为使物块能到达轨道的最高点C，求物块在传送带上运动时间最短时的传送带长度。
如图所示，空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场，电场强度为E、宽度为L。在紧靠电场右侧的圆形区域内，分布着垂直于纸面向外的匀强磁场，圆形磁场区域半径为r。当一带正电的粒子（质量为m，电荷量为q）从A点静止释放后，在M点离开电场，并沿半径方向射入磁场区域，磁感应强度为B，粒子恰好从N点射出，O为圆心，∠MON＝120°，粒子重力忽略不计。求：
（1）粒子经电场加速后，进入磁场时速度v的大小；
（2）匀强磁场的磁感应强度B的大小和粒子在电场、磁场中运动的总时间t；
（3）若粒子在离开磁场前某时刻，磁感应强度方向不变，大小突然变为B1，此后粒子恰好被束缚在该磁场中，则B1的最小值为多少？
如图所示，两条平行的光滑金属导轨固定在倾角为θ的绝缘斜面上，导轨间距为L，导轨上端连接一个阻值为3Ω的定值电阻R。在水平虚线L1、L2间有一与导轨所在斜面垂直向上的匀强磁场B，磁场区域的宽度为d。导体棒a、b放在斜面上，a棒的质量ma=0.2kg，电阻Ra=2Ω；b棒的质量mb=0.1kg，电阻Rb=2Ω，它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动，都能匀速穿过磁场区域，且当b棒刚穿出磁场时a棒正好进入磁场。重力加速度g=10m/s2，不计棒之间的相互作用，不计金属导轨的电阻。导体棒始终与导轨垂直且与导轨接触良好，导轨足够长。求：
（1）安培力对导体棒a、b的作功之比Wa:Wb为多少。
（2）导体棒a、b在磁场中运动时速度之比va:vb为多少。
（3）如果d=0.4m，则a棒开始运动时距虚线L1的距离la是多少？
如图所示，在半径为R的圆形边界内存在竖直向上的匀强电场，电场强度E=1×106T。以圆心为坐标原点建立直角坐标系，在坐标原点分别以竖直向上、竖直向下，水平向左、水平向右同时抛出四个带正电的小球，小球的电荷量q=8×10-12C，质量m=1×10-6kg，它们的初速度大小均为v0=4m/s，忽略空气阻力，重力加速度g="10m/" s2。则：
（1）当R=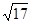
m时，水平向右抛出的小球经过多少时间到达圆形边界？
（2）试证明，在四个小球都未到达圆形边界前，能用一个圆将四个小球连起来。并写出圆心的坐标。
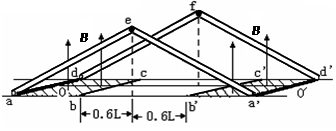
如图所示，由六根质量不计的导体棒组成一个人字形线圈，放在光滑绝缘水平面上，每根导棒长均为L=1m，线圈总电阻R=0.2Ω，将ad与a/d/用细线OO/拉住，e、f是两个质量都为m=0.1kg光滑转轴，四根倾斜导体棒与水平面成37 0角。人字形线圈在水平面投影区内有两块对称的区域，竖直向上的匀强磁场B穿过这两块区域。如图中阴影区域所示（ad与a/d/恰在磁场中），其他地方没有磁场。磁场按B=
+0.5t 的规律变化，取sin37°＝0.6，cos37°＝0.8。求：
（1）t=0时水平面对线圈ad边支持力的大小和此时通过线圈电流大小；
（2）经过多少时间线圈的ad边与a/d/边开始运动？
（3）若在磁场力作用下经过一段时间，当线圈中产生了Q=1.2J热量后线圈刚好能完全直立（即ad边与a/d/边并拢在一起），则在此过程中磁场对线圈总共提供了多少能量？
（4）若人形线圈从直立状态又散开，此时磁感强度为B0 =T且不再变化，则ad边与a/d/再次刚进入磁场时，通过线圈的电流为多大？