如图(1),小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图(2)),量得他们的斜边长为10cm,较小锐角为30.再将这两张三角纸片摆成如图(3)的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图(3)至图(6)中统一用F表示)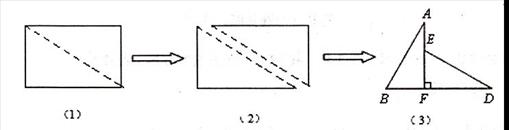
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图(3)中△ABF沿BD向右平移到图(4)的位置,使点B与点F重合,请你求出平移的距离;
(2)将图(3)中△ABF绕点F顺时针方向旋转30°到图(5)的位置,A.F交DE于点G,请你求出线段FG的长度;
(3)将图(3)中的△ABF沿直线AF翻折到图(6)的位置,AB,交DE丁点H,请证明:AH=DH.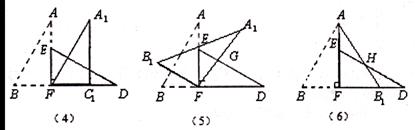
某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容。规定:每位考生先在三个笔试题(题签分别用代码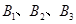 表示)中抽取一个,再在三个上机题(题签分别用代码
表示)中抽取一个,再在三个上机题(题签分别用代码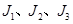 表示)中抽取一个进行考试。小亮在看不到题签的情况下,分别从笔试题和上机题中随机地各抽取一个题签。
表示)中抽取一个进行考试。小亮在看不到题签的情况下,分别从笔试题和上机题中随机地各抽取一个题签。
(1)用树状图或列表法表示出所有可能的结构;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“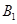 ”的下表为“1”)均为奇数的概率。
”的下表为“1”)均为奇数的概率。
如图,已知直线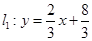 与直线
与直线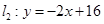 相交于点
相交于点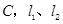 分别交
分别交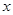 轴
轴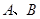 两点.矩形
两点.矩形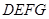 的顶点
的顶点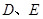 分别在直线
分别在直线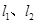 上,顶点
上,顶点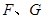 都在
都在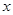 轴上,且点
轴上,且点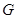 与点
与点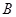 重合.
重合.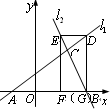
(1)求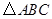 的面积;
的面积;
(2)求矩形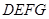 的边
的边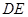 与
与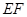 的长;
的长;
(3)若矩形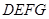 从原点出发,沿
从原点出发,沿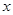 轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形
轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t<3)秒,矩形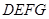 与
与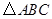 重叠部分的面积为
重叠部分的面积为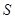 ,求
,求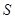 关于的函数关系式.
关于的函数关系式.
如图:已知AB是⊙O的直径,P为AB的延长线上一点.且BP=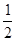 AB,C、D是半圆AB的两个三等分点,连接PD.
AB,C、D是半圆AB的两个三等分点,连接PD.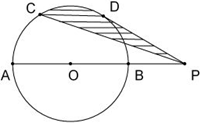
(1)PD与⊙O有怎样的位置关系?并证明你的结论;
(2)连接PC,若AB=10cm,求由PC,弧CD、PD所围成的图形的面积(结果保留π).
先阅读理解下面的例题,再按要求解答后面的问题
例题:解一元二次不等式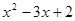 >0.解:令y=
>0.解:令y=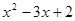 ,画出y=
,画出y=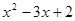 如图所示,
如图所示,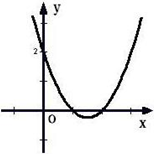
由图像可知:当x<1或x>2时,y>0.所以一元二次不等式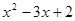 >0的解集为x<1或x>2.
>0的解集为x<1或x>2.
填空:(1)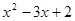 <0的解集为;
<0的解集为;
(2)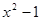 >0的解集为;
>0的解集为;
用类似的方法解一元二次不等式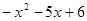 >0.
>0.
如图,在矩形ABCD(AB<AD)中,将△ABE沿AE对折,使AB边落在对角线AC上,点B的对应点为F,同时将△CEG沿EG对折,使CE边落在EF所在直线上,点C的对应点为H.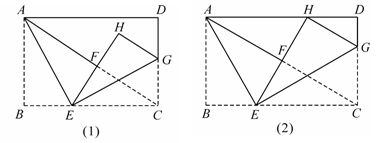
(1)证明:AF∥HG(图(1));
(2)如果点C的对应点H恰好落在边AD上(图(2)).判断四边形AECH的形状,并说明理由.