已知数列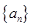 的前
的前 项和为
项和为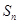 ,且
,且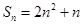 ,
,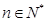 ,数列
,数列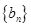 满足
满足 ,
,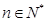 .
.
(1)求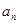 ,
, ;
;
(2)求数列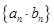 的前
的前 项和
项和 .
.
(1)求证:平面ACD⊥平面ABC;
(2)求二面角C-AB-D的大小。
(1)证明数列{an-n}是等比数列;
(2)求数列{an}的前n项和Sn;
(3)证明不等式Sn+1≤4Sn,对任意n∈N*皆成立。
| 产品A(件) |
产品B(件) |
||
| 研制成本、搭载费用之和(万元) |
20 |
30 |
计划最大资金额300万元 |
| 产品重量(千克) |
10 |
5 |
最大搭载重量110千克 |
| 预计收益(万元) |
80 |
60 |
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
已知直线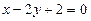 经过椭圆
经过椭圆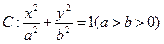

的左顶点A和上顶点D,椭圆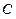 的右顶点为
的右顶点为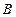 ,点
,点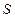 和椭
和椭
圆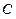 上位于
上位于 轴上方的动点,直线,
轴上方的动点,直线,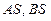 与直线
与直线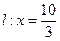
分别交于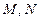 两点。
两点。
(I)求椭圆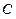 的方程;
的方程;
(Ⅱ)求线段MN的长度的最小值;
(Ⅲ)当线段MN的长度最小时,在椭圆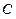 上是否存在这
上是否存在这
样的点 ,使得
,使得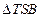 的面积为
的面积为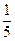 ?若存在,确定点
?若存在,确定点 的个数,若不存在,说明理由
的个数,若不存在,说明理由
已知以原点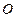 为中心的双曲线的一条准线方程为
为中心的双曲线的一条准线方程为 ,离心率
,离心率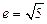 .
.
(Ⅰ)求该双曲线的方程;
(Ⅱ)如图,点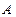 的坐标为
的坐标为 ,
,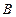 是圆
是圆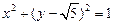 上的点,点
上的点,点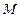 在双曲线右支上,求
在双曲线右支上,求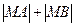 的最小值,并求此时
的最小值,并求此时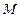 点的坐标;
点的坐标;

