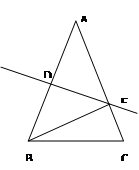如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒（A、B、C、D四个顶点正好重合于上底面上一点）。已知E、F在ＡＢ边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x(cm).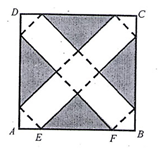
（1）若折成的包装盒恰好是个正方体，试求这个包装盒的体积V；
（2）某广告商要求包装盒的表面（不含下底面）面积S最大，试问x应取何值？S最大值是多少？
如图,直线y = kx+6与x轴y轴分别相交于点E、F. 点E的坐标为(- 8, 0), 点A的坐标为(- 6,0). 点P（x,y）是第二象限内的直线上的一个动点。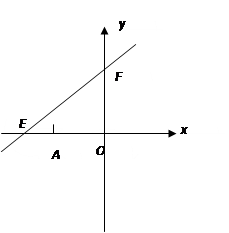
(1)求k的值；
(2)当点P运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
(3)探究：当P运动到什么位置（求P的坐标）时，△OPA的面积为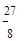
，并说明理由
如图，在平面直角坐标系中，函数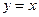
的图象
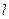是第一、三象限的角平分线．
实验与探究：由图观察易知A（0，2）关于直线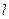的对称点
的
坐标为（2，0），请在图中分别标明B(5,3) 、C(-
2,5) 关于直线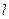的对称点
、
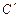的位置，并写出它们的坐标: 、；
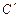归纳与发现：结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(m,n)关于第一、三象限的角平分线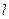的对称点
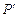的坐标为；
运用与拓广：已知两点D(0,-3)、E(-1,-4)，试在直线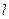上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标
如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．
(1)求证：AB＝DC；
(2)试判断△OEF的形状，并说明理由
如图，矩形ABCD中，△ABC沿AC折叠，点B落在B＇的位置，CB＇与AD交于点O，求证：△AOC是等腰三角形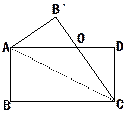
在△ABC中，AB=AC，DE垂直平分AB，且分别交AB、AC于D、E，
若∠A=40°，求∠EBC的度数