若对任意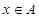 ,
,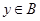 ,(
,(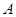 、
、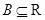 )有唯一确定的
)有唯一确定的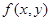 与之对应,称
与之对应,称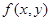 为关于
为关于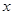 、
、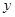 的二元函数. 现定义满足下列性质的二元函数
的二元函数. 现定义满足下列性质的二元函数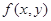 为关于实数
为关于实数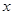 、
、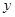 的广义“距离”:
的广义“距离”:
(1)非负性: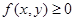 ,当且仅当
,当且仅当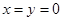 时取等号;
时取等号;
(2)对称性: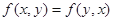 ;
;
(3)三角形不等式: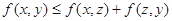 对任意的实数z均成立.
对任意的实数z均成立.
今给出四个二元函数:①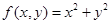 ;②
;②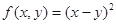 ③
③ ;
;
④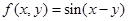 .
.
能够成为关于的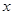 、
、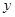 的广义“距离”的函数的所有序号是 .
的广义“距离”的函数的所有序号是 .
已知整数对的序列如下:
(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…则第60个数对是____________
我们把平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为斜坐标系.平面上任意一点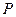 的斜坐标定义为:若
的斜坐标定义为:若 (其中
(其中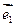 、
、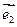 分别为斜坐标系的
分别为斜坐标系的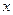 轴、
轴、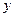 轴正方向上的单位向量,
轴正方向上的单位向量,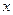 、
、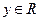 ),则点
),则点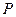 的斜坐标为
的斜坐标为 .在平面斜坐标系
.在平面斜坐标系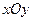 中,若
中,若 ,已知点
,已知点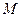 的斜坐标为
的斜坐标为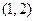 ,则点
,则点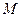 到原点
到原点 的距离为.
的距离为.
 的值是.
的值是.
若函数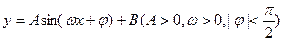 的最大值是
的最大值是 ,最小值是
,最小值是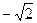 ,最小正周期是
,最小正周期是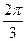 ,图象经过点(0,-
,图象经过点(0,-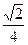 ),则函数的解析式子是.
),则函数的解析式子是.
若 ,则与
,则与 垂直的单位向量的坐标为__________.
垂直的单位向量的坐标为__________.