先阅读，后解答：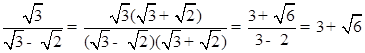
像上述解题过程中，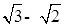
与
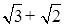相乘，积不含有二次根式，我们可将这两个式子称为互为有理化因式，上述解题过程也称为分母有理化，
（1）
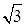的有理化因式是 ； 
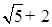的有理化因式是 ．
（2）将下列式子进行分母有理化：
（1）
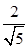= ；（2）
= ．
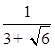（3）已知a=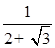
,b=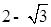
，比较a与b的大小关系．
如图，小区计划在一个长为40cm，宽为26m的矩形场地ABCD上修建三条同样宽的路，使其中两条与AB平行，另一条与AD平行，其余部分种草，若使每一块草坪的面积都为144m2，求路的宽度．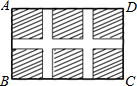
如图，在平面直角坐标系中，一次函数y=﹣2x的图象与反比例函数y=
的图象的一个交点为A（﹣1，n）．
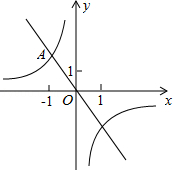
（1）求反比例函数y=的解析式；
（2）若P是x轴上一点，且满足△AP0为等腰三角形，直接写出点P的坐标．
如图，已知A（﹣4，2）、B（n，﹣4）是一次函数y=kx+b的图象与反比例函数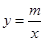
的图象的两个交点．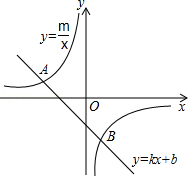
（1）求此反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．
已知a、b是实数，且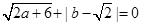
，解关于x的方程：（a+2）x2+b2=（a﹣1）x．
用适当的方法解下列方程：
（1）（5x+3）2﹣4=0
（2）2x2+4x﹣3=0．