如图甲所示，倾角为θ的光滑斜面体固定在水平面内，经度系数为k的轻弹簧，一端固定在斜面底端，另一端与质量为m的小滑块接触但不栓接，现用沿斜面向下的力F推滑块至离地高度h0处，弹簧与斜面平行，撤去力F，滑块沿斜面向上运动，其动能Ek和离地高度h的变化关系如图乙所示，图中h2对应图线的最高点，h3到h4范围内图线为直线，其余部分为曲线，重力加速度为g，则
| A．h1高度处，弹簧形变量为 |
B．h2高度处，弹簧形变量为 |
| C．h0高度处，弹簧的弹性势能为mg(h3-h0) |
| D．h1高度处，弹簧的弹性势能为mg(h3-h1) |
地球同步卫星的质量为m,离地面的高度为h，地球表面的重力加速度为g，地球半径为R，地球自转的角速度为ω，那么同步卫星所受地球对它的万有引力的大小为（）
| A．0 | B． |
C． |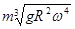
D．以上结果都不正确 |
关于“探究功与物体速度变化的关系”实验中，下列
叙述正确的是（）
| A．每次实验必须设法算出橡皮筋对小车做功的具体数值 |
B．每次实 验中，橡皮筋拉伸的长度没有必要保持一致 |
| C．放小车的长木板应该尽量使其水平 |
| D．先接通电源，再让小车在橡皮筋的作用下弹出 |
如图，细杆的一端与一小球相连，可绕过O点的水平轴自由转动,现给小球一初速度，使它做圆周运动，图中a、b分别表示小球轨道的最低点和最高点，则杆对球的作用力可能是（）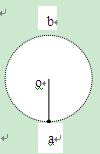
| A．a处为拉力，b处为拉力 | B．a处为拉力，b处为推力 |
| C．a处为推力，b处为拉力 | D．a处为推力，b处为推力 |
一飞船在某行星表面附近沿圆轨道绕该行星飞行,认为行星是密度均匀的球体,要确定该行星的密度,只需要测量（）
| A．飞船的轨道半径 | B．飞船的运行速度 |
| C．飞船的运行周期 | D．行星的质量 |
如图所示，半径为r的圆桶，绕其竖直中心轴OO/转
动，小物块a靠在圆筒的内壁上，它与圆筒间的动摩擦因数为μ,现要使小物块不下落，圆筒转动的角速度ω至少为 ( )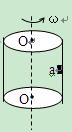
A． |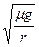
B． |
C． |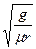
D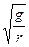． |