(18分) 如图所示，一半径为R＝1.00 m的水平光滑圆桌面，圆心为O，有一竖直立柱，其横截面为圆形，半径为r＝0.1 m，圆心也在O点。一根长l＝0.757 m的细轻绳，一端固定在圆柱上的A点，另一端系一质量为m＝0.075kg的小球，将小球放在桌面上并将绳沿半径方向拉直，再给小球一个方向与绳垂直，大小为v0＝4 m/s的初速度。小球在桌面上运动时，绳子将缠绕在圆柱上。已知绳子的张力为T0＝2 N时，绳就被拉断，在绳断开前球始终在桌面上运动。试求：
(1)绳刚要断开时，绳的伸直部分的长度为多少；
(2)小球最后从桌面上飞出时，飞出点与开始运动的点B之间的距离为多少。(结果保留3位有效数字)
如图15-4所示，区域Ⅰ和区域Ⅱ的匀强磁场磁感应强度大小相等、方向相反.在区域Ⅱ的A处有一静止的原子核发生α衰变，生成的新核电荷量为q（大于α粒子带电荷量），新核和α粒子的运动轨迹如图，其中一个由区域Ⅱ进入区域Ⅰ，与光滑绝缘挡板PN垂直相碰后（PN与磁场分界线CD平行），经过一段时间又能返回到A处，已知区域Ⅰ的宽度为d，试求新核和α粒子的轨道半径.（基元电荷电荷量为e）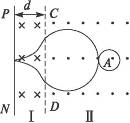
图15-4
一个静止的氮核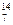
N俘获一个速度为2.3×107 m/s的中子生成一个复核A，A又衰变成B、C两个新核.设B、C的速度方向与中子速度方向相同，B的质量是中子的11倍，速度是106 m/s，B、C在同一匀强磁场中做圆周运动的半径比RB∶RC=11∶30.求：
(1)C核的速度大小；
(2)根据计算判断C核是什么.
(3)写出核反应方程式.
对于自由落体运动，1秒钟下落的高度是9.8吗？；相邻两秒钟内的位移之差是9.8m吗？
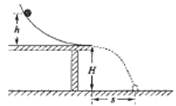
某同学利用如图所示的实验装置验证机械能守恒定律。弧形轨道末端水平，离地面的高度为
。将钢球从轨道的不同高度
处静止释放，钢球的落点距轨道末端的水平距离为
。
（1）若轨道完全光滑，
与
的理论关系应满足
＝(用
、
表示)。
（2）该同学经实验测量得到一组数据，如下表所示：
| h(10－１m) |
2.00 |
3.00 |
4.00 |
5.00 |
6.00 |
| s2 (10－１ｍ２) |
2.62 |
3.89 |
5.20 |
6.53 |
7.78 |
请在坐标纸上作出
关系图。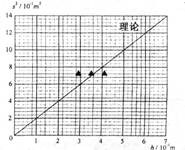
（3）对比实验结果与理论计算得到的
关系图线(图中已画出)，自同一高度静止释放的钢球，水平抛出的速率(填"小于"或"大于")理论值。
（4）从
关系图线中分析得出钢球水平抛出的速率差十分显著，你认为造成上述偏差的可能原因是。
在LC振荡电路中，如已知电容C，并测得电路的固有振荡周期T，即可求得电感L.为了提高测量精度，需多次改变C值并测得相应的T值，现将测得的六组数据标示在以C为横坐标、T2为纵坐标的坐标纸上，即图14-2-11所示中用“×”表示的点.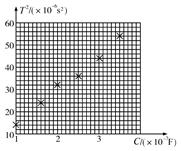
图14-2-11
（1）T、L、C的关系为____________.
（2）根据图中给出的数据画出T2与C的关系图线.
（3）求得的L值是____________.