如图所示为研究电子枪中电子在电场中运动的简化模型示意图．在xOy平面的第一象限，存在以x轴、y轴及双曲线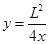
的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ；在第二象限存在以x＝－L、x＝－2L、y＝0、y＝L的匀强电场区域Ⅱ.两个电场大小均为E，不计电子所受重力，电子的电荷量为e，则：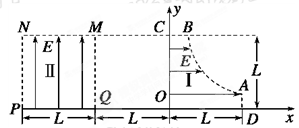
(1)求从电场区域Ⅰ的边界B点（B点的纵坐标为L）处由静止释放电子，到达区域Ⅱ的M点时的速度；
(2) 求（1）中的电子离开MNPQ时的坐标；
(3)证明在电场区域Ⅰ的AB曲线上任何一点处，由静止释放电子恰能从MNPQ区域左下角P点离开；
一细杆与水桶相连，水桶中装有水，水桶与细杆一起在竖直平面内做圆周运动，如图所示，水的质量m＝0.5kg，水的重心到转轴的距离l＝50cm。（取g＝10m/s2，不计空气阻力）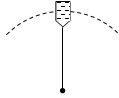
⑴若在最高点水不流出来，求桶的最小速率；
⑵若在最高点水桶的速率v＝3m/s，求水对桶底的压力。
如图所示，射击枪水平放置，射击枪与目标靶中心位于离地面足够高的同一水平线上，枪口与目标靶之间的距离s＝100m，子弹射出的水平速度v＝200m/s，子弹从枪口射出的瞬间目标靶由静止开始释放，不计空气阻力，取重力加速度g为10 m/s2，求：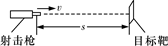
(1)从子弹由枪口射出开始计时，经多长时间子弹击中目标靶？
(2)目标靶由静止开始释放到被子弹击中，下落的距离h为多少？
如图所示，在光滑的圆锥体顶端用长为L的细线悬挂一质量为m的小球。圆锥体固定在水平面上不动，其轴线沿竖直方向，母线与轴线之间的夹角θ＝300。现使小球以一定的速率绕圆锥体的轴线在水平面内做圆周运动.
（1）当小球速率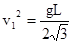
时，求细线对小球的拉力；
（2）当小球速率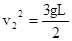
时，求细线对小球的拉力。
如图所示，两小球a、b从直角三角形斜面的顶端以相同大小的水平速率v0向左、向右水平抛出，分别落在两个斜面上，三角形的两底角分别为30°和60°，则两小球a、b运动时间之比为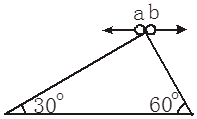
已知地球表面的重力加速度为g，地球半径为R，地球自转周期为T，试求地球同步卫星轨道距地面的高度。