如图，在海岸线一侧C处有一个美丽的小岛，某旅游公司为方便游客，在上设立了A、B两个报名点，满足A、B、C中任意两点间的距离为10千米。公司拟按以下思路运作：先将A、B两处游客分别乘车集中到AB之间的中转点D处（点D异于A、B两点），然后乘同一艘游轮前往C岛。据统计，每批游客A处需发车2辆，B处需发车4辆，每辆汽车每千米耗费2元，游轮每千米耗费12元。设∠
，每批游客从各自报名点到C岛所需运输成本S元。
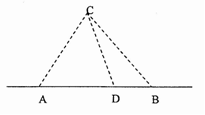
⑴写出S关于
的函数表达式，并指出的取值范围；
⑵问中转点D距离A处多远时，S最小？
试比较下列各式的大小（不写过程）
（1）
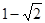与
（2）与
通过上式请你推测出
与
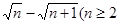且n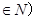
的大小，并用分析法加以证明。
假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计资料：
| x |
2 |
3 |
4 |
5 |
6 |
| y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料可知y对x呈线性相关关系。试求：
（1）线性回归方程；
（2）估计使用年限为10年时，维修费用是多少？
已知复数z="(2+i)(i-3)+4-2i;"
(1)求复数z的共轭复数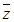
及||；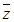
(2)设复数z1=(a2-2a)+ai是纯虚数，求实数a的值
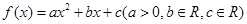已知函数
，若函数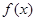
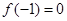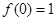的最小值是
，
且对称轴是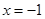
（1）设
求
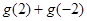的值；
（2）在（1）条件下求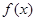在区间
的最小值.
已知集合A＝
x|x>a
，集合B＝
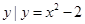
．若B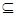
A，则实数a的取值范围是a多少？