下列命题:①至少有一个x使x2+2x+1=0成立;②对任意的x都有x2+2x+1=0成立;
③对任意的x都有x2+2x+1=0不成立;④存在x使x2+2x+1=0成立.
其中是全称命题的有( )
| A.1个 | B.2个 | C.3个 | D.0个 |
设集合 ,集合
,集合 ,则
,则 ()
()
A. |
B. |
C. |
D. |
已知全集U=R,集合M={x||x-1| 2},则
2},则 =( )
=( )
| A.{x|-1<x<3} | B.{x|-1 x x 3} 3} |
C.{x|x<-1或x>3} | D.{x|x -1或x -1或x 3} 3} |
设z的共轭复数是 ,z+
,z+ =4,z·
=4,z· =8,则
=8,则 等于( )
等于( )
| A.1 | B.-i | C.±1 | D.±i |
.如果复数 为纯虚数,那么实数a的值为( )
为纯虚数,那么实数a的值为( )
| A.1 | B.2 | C.-2 | D.1或-2 |
已知定义在R上的奇函数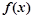 满足
满足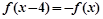 ,且
,且 时,
时, ,甲,乙,丙,丁四位同学有下列结论:甲:
,甲,乙,丙,丁四位同学有下列结论:甲: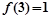 ;乙:函数
;乙:函数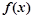 在[-6,-2]上是增函数;丙:函数
在[-6,-2]上是增函数;丙:函数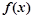 关于直线
关于直线 对称;丁:若
对称;丁:若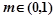 ,则关于x的方程
,则关于x的方程 在[-8,8]上所有根之和为-8,其中正确的是
在[-8,8]上所有根之和为-8,其中正确的是
| A.甲,乙,丁 | B.乙,丙 | C.甲,乙,丙 | D.甲,丁 |