如图,五面体中,四边形ABCD是矩形,DA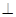 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF, ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.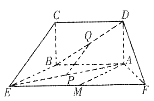
(1)求证:PQ//平面BCE;
(2)求证:AM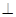 平面ADF;
平面ADF;
(3)求二面角A-DF-E的余弦值.
一个正三棱柱的三视图如图所示,求这个三棱柱的表面积和体积.
已知△ABC的直观图A′B′C′是边长为a的正三角形,求原三角形ABC的面积.
.已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,左视图(或称侧视图)是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;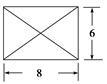
(2)求该几何体的侧面积S.
某旅游商品生产企业,2007年某商品生产的投入成本为1元/件,出厂价为1.2元/件,年销售量为10000件,因2008年调整黄金周的影响,此企业为适应市场需求,计划提高产品档次,适度增加投入成本。若每件投入成本增加的比例为 (
( ),则出厂价相应提高的比例为
),则出厂价相应提高的比例为 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为 。已知年利润
。已知年利润 (出厂价
(出厂价 投入成本)
投入成本) 年销售量。
年销售量。
(1)写出2008年预计的年利润 与投入成本增加的比例
与投入成本增加的比例 的关系式;
的关系式;
(2)为使2008年的年利润达到最大,则每件投入成本增加的比例 应是多少?此时最大年利润是多少?
应是多少?此时最大年利润是多少?
已知函数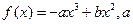 、
、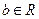 。
。
(1)讨论函数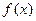 的奇偶性(只写结论,不要求证明);
的奇偶性(只写结论,不要求证明);
(2)在构成函数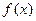 的映射
的映射 中,当输入值为
中,当输入值为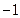 和2时分别对应的输出值为
和2时分别对应的输出值为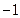 和
和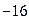 ,求
,求 、
、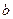 的值;
的值;
(3)在(2)的条件下,求函数 (
(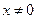 )的最大值。
)的最大值。