经市场调查,某种优质西瓜质量为(5±0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A、B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗,记录它们的质量如下(单位:kg):
(1)若质量为(5±0.25)kg的为优等品,根据以上信息完成下表:
| |
优等品数量(颗) |
平均数 |
方差 |
| A |
|
5.0 |
0.103 |
| B |
|
5.0 |
0.093 |
(2)请分别从优等品数量、平均数与方差三方面对A、B两种技术作出评价;从市场销售的角度看,你认为推广哪种种植技术较好.
在□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
求证:△BEC≌△DFA;
连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论
解方程: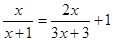 .
.
计算

去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最少可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
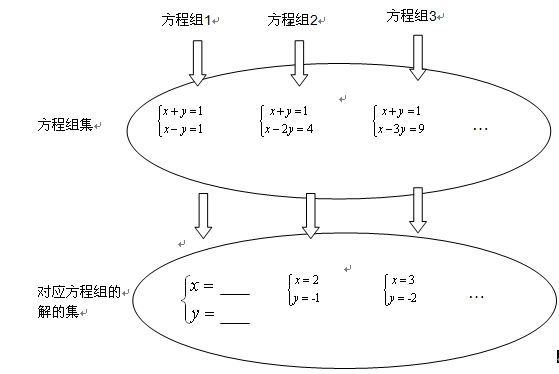
下图是按一定规律排列的方程组集和它的解的集的对应关系图,若方程组集中的方程组自左至右依次记作:方程组1、方程组2、方程组3……方程组n,
(1)将方程组1的解填入图中。
(2)若方程组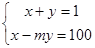 的解是
的解是 ,求m的值。
,求m的值。
(3)请依据方程组的变化规律写出方程组n(n为正整数),并解这个方程组。