已知：如图①，在Rt△ACB中，∠C=90°，AC=4cm，BC=3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t(s)（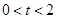
），解答下列问题：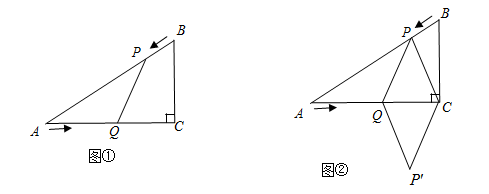
（1）当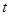
为何值时，PQ∥BC？
（2）设△AQP的面积为y（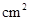
），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；
（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻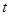，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．
如图，在△ABE与△ACD中，点D在AB上，点E在AC上，BE和CD相交于点O，若AB=AC， BD=CE，则∠ADC=∠AEB.请说明理由。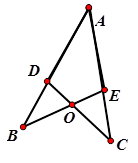
如图：在正方形网格中有一个△ABC，请按下列要求进行（只能借助于网格）：
（1）、请作出△ABC中BC边上的高AE；
（2）、作出将△ABC向右平移6格，再向上平移3格后的△DEF；
（3）、作一个锐角△MNP（要求各顶点在格点上），使其面积等于△ABC的面积。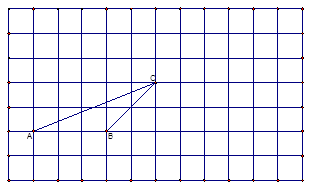
如图，在△ABC中，点D为BC边上的点，BE平分∠ABC交AD于点E．若∠ABE=15°，∠BAD=40°，求∠ADC的度数。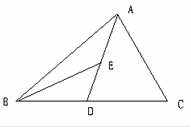
如图，M是AB的中点，∠C=∠D，∠1=∠2，请说明 AC=BD的理由（填空）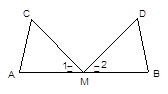
解：
M是AB的中点，
∴ AM = ( )
在
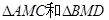中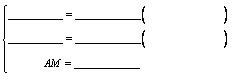
∴△≌△（）
∴AC=BD（）
解下列方程组：
（1）
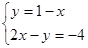；（2）