某中学为调查本校学生周末平均每天做作业所用时间的情况，随机调查了50名同学，下图是根据调查所得数据绘制的统计图的一部分．
请根据以上信息，解答下列问题：
（1）在这次调查的数据中，做作业所用时间的众数是 ，中位数是 ，平均数是 ；
（2）若该校共有2000名学生，根据以上调查结果估计该校全体学生每天做作业时间在3小时内（含3小时）的同学共有多少人?
（1）求不等式组
的整数解；
（2）化简：
．
（1）计算：﹣12014+
﹣（
）﹣1；
（2）解方程：
．
二次函数y=x2-2mx+3（m＞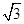
）的图象与x轴交于点A（a，0）和点B（a+n，0）（n＞0且n为整数），与y轴交于C点．
（1）若a=1，①求二次函数关系式；②求△ABC的面积；
（2）求证：a=m-
；
（3）线段AB（包括A、B）上有且只有三个点的横坐标是整数，求a的值．
如图，已知△ABD为⊙O的内接正三角形，AB=2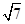
，E、F分别为边AD、AB上的动点，且AE=BF，DF与BE相交于G点，过B点作BC∥DF交
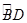于点C，连接CD．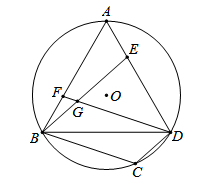
（1）求∠BCD的度数；
（2）求证：四边形BCDG为平行四边形；
（3）连接CG，当CG与△BCD的一边垂直时，求CG的长度．
甲乙两地相距400km，一辆轿车从甲地出发，以一定的速度匀速驶往乙地．0．5h后，一辆货车从乙地出发匀速驶往甲地（轿车的速度大于货车的速度），与轿车在途中相遇．此后，两车继续行驶，并各自到达目的地．两车之间的距离y（km）与轿车行驶的时间x（h）的函数图象如图．
（1）解释D点的实际意义并求两车的速度；
（2）求m、n的值；
（3）若两车相距不超过180千米时能够保持联系，请问货车在行驶过程中与轿车保持联系的时间有多长？