用反证法证明：若整系数一元二次方程ax2＋bx＋c＝0(a≠0)有有理数根，那么a、b、c中至少有一个是偶数．用反证法证明时，下列假设正确的是( )
| A．假设a、b、c都是偶数 | B．假设a、b、c都不是偶数 |
| C．假设a、b、c至多有一个偶数 | D．假设a、b、c至多有两个偶数 |
若复数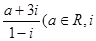
是虚数单位)是纯虚数，则实数a的值为( )
| A．-3 | B．3 | C．-6 | D．6 |
在区间［0,1］上任意取两个实数a，b，则函数f(x) ＝
在区间［-1，1］上有且仅有一个零点的概率为
A． |
B． |
C． |
D． |
如图，F1，F2是双曲线
的左、右焦点，过F1的直线l与C的左、右两支分别交于A，B两点．若｜AB｜：｜BF2｜：｜AF2｜=3：4：5，则双曲线的离心率为
A． |
B． |
C．2 | D． |
某程序框图如图所示，则该程序运行后输出的S的值为
| A．1 | B． |
C． |
D． |
，若
，有
，则
的取值范围是（ ）
