已知:如图,直线 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.
相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.
(1)求点P的坐标;
(2)请判断△OPA的形状并说明理由;
(3)请探究S与t之间的函数关系式,并指出t的取值范围.
某中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调整兴趣活动小组,为此进行了一次抽样调查,根据采集到的数据绘制的统计图(不完整)如下:
请你根据图中提供的信息,完成下列问题:
(1)图1中,“电脑”部分所对应的圆心角为 _________ 度;
(2)共抽查了 _________ 名学生;
(3)在图2中,将“体育”部分的图形补充完整;
(4)爱好“书画”的人数占被调查人数的百分比 _________ ;
(5)估计现有学生中,有 _________ 人爱好“书画”.
两位搬运工人要将若干箱同样的货物用电梯运到楼上.已知一箱货物的质量是65千克,两位工人的体重之和是150千克,电梯的载重量是1800千克,问两位工人一次最多能运多少箱货物?
如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
(1)建立以点B为原点,AB边所在直线为x轴的直角坐标系.写出点A、B、C、D的坐标;
(2)求出四边形ABCD的面积;
(3)请画出将四边形ABCD向上平移5格,再向左平移2格后所得的四边形A′B′C′D′.
如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知)
∴∠2= _________ ( )
又∵∠1=∠2(已知)
∴∠1=∠3( )
∴AB∥ _________ ( )
∴∠BAC+ _________ =180°( )
∵∠BAC=70°(已知)
∴∠AGD= _________ .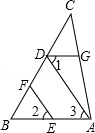
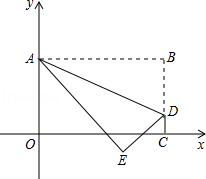
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,求点B的坐标和点E的坐标;(自己重新画图)
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.