已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时(如图1)易证:AB=CG+CE.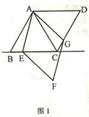
(1)当点在E线段BC的延长线上时(如图2),猜想AB、CG、CE之间的关系并证明;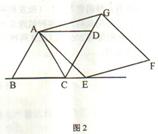
(2)当点在E线段CB的延长线上时(如图3),猜想AB、CG、CE之间的关系.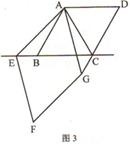
一个铜球在0℃时的体积是1000cm3,加热后温度增加1℃,体积增加0.051cm3,写出铜球的体积V与t之间的函数关系式,并计算加热到200℃时铜球的体积.
某空军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油过程中,设运输飞机的油箱余量为Q1吨,加油飞机的加油油箱剩余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题: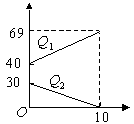
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需要多少分钟?
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分钟)的函数关系式.
如图所示,折线ABC是某城市出租车所收车费y(元)与出租车行驶路程x(千米)之间的函数关系的图像.根据图像,求: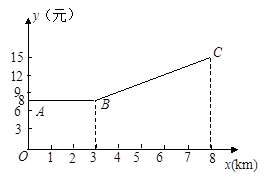
(1)当x≥3时,y与x之间的函数关系式;
(2)某人乘车2km应付车费多少元?
(3)若某人付车费10.8元,则出租车行驶了多少千米?
某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司其中的一家签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月租费用是y1元,应付给出租公司的月租费用是y2元,y1、y2分别与x之间的函数关系图像(两条射线)如图所示,观察图像回答下列问题:
(1)每月行驶的路程在什么范围内时,租国有公司的车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
张师傅驾车运送货物到某地出售,汽车出发前油箱有油50升,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
请根据图象回答下列问题: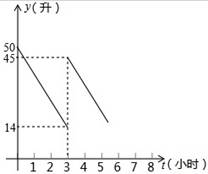
(1)汽车行驶______小时后加油,中途加油______升;
(2)已知加油前、后汽车都以70千米/小时匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否够用?请说明理由.