我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图（3）可以用来解释（a+b）2－（a－b）2=4ab.那么通过图（4）面积的计算，验证了一个恒等式，此等式是（）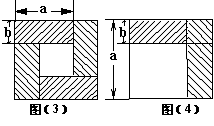
| A．a2－b2=（a+b）（a－b） |
| B．（a－b）2=a2－2ab+b2 |
| C．（a+b）2=a2+2ab+b2 |
| D．（a－b）（a+2b）=a2+ab－b2 |
如图，小方格的面积是1，则图中以格点为端点且长度为5的线段有（）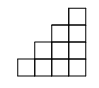
| A．4条 | B． 3条 | C． 2条 | D．1条 |
已知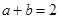
，则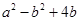
的值是（ ）
A． |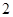
B． |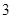
C． |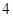
D． |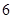
若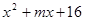
是一个完全平方式,则
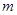的取值是（ )
| A．8 | B． |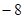
C． |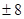
D． |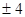
下列式子，总能成立的是（）
A． |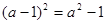
B． |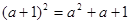
C． |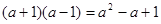
D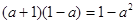． |