(11分)光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板（平面部分足够长），滑板的质量为4m。距离滑板的右壁A为L1的B处放有一质量为m、电量为+q(q>0)的小物体（可视为质点），小物体与板面之间的摩擦可忽略不计。整个装置处于场强为E、方向水平向右的匀强电场中。开始时，滑板与小物体都处于静止状态，某时刻释放小物体，求：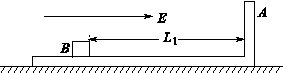
（1）小物体第一次跟滑板的A壁碰撞前瞬间的速度v1多大;
（2）若小物体与A壁碰撞时间极短，且碰撞过程没有机械能损失，则
a.小物体第二次即将跟A壁碰撞瞬间，滑板的速度v和小物体的速度v2分别为多大;
b.从开始释放小物体到它即将第二次跟A壁碰撞的过程中，整个装置的电势能减少了多少.
如图所示，一子弹以水平速度射入放置在光滑水平面上原来静止的木块，并留在木块中，在此过程中子弹钻入木块的深度为d，木块的位移为s，木块对子弹的摩擦力大小为f，求（1）木块对子弹的摩擦力做的功（2）子弹对木块的摩擦力做的功
水平地面上一质量m=10Kg的物体在大小为30N的水平恒力F的作用下从静止开始运动了10m，之后撤去F，已知物体与地面的动摩擦因素μ等于0.1，g取10m/s2,问物体还能继续滑行多长距离？
荡秋千是大家喜爱的一项体育活动。随着科技的迅速发展，将来的某一天，同学们也许会在其它星球上享受荡秋千乐趣。假设你当时所在星球的质量是M、半径为R，可将人视为质点，秋千质量不计、摆长不变、摆角小于90°，万有引力常量为G。那么，
（1）该星球表面附近的重力加速度
等于多少？
（2）若经过最低位置的速度为v0，你能上升的最大高度是多少？
如图所示，电阻不计的平行金属导轨MN和OP放置在水平面内．MO间接有阻值为R = 3Ω的电阻．导轨相距d = 1m，其间有竖直向下的匀强磁场，磁感强度B = 0.5T．质量为m = 0.1kg，电阻为r = 1Ω的导体棒CD垂直于导轨放置，并接触良好，现用平行于MN的恒力F = 1N向右拉动CD，CD受摩擦阻力f恒为0.5N．求
（1）CD运动的最大速度是多少？
（2）当CD达到最大速度后，电阻R消耗的电功率是多少？
（3）当CD的速度为最大速度的一半时，CD的加速度是多少？
如图，匀强磁场的磁感应强度方向垂直于纸面向里，大小随时间的变化率
，
为正的常量。用电阻率为
、横截面积为
的硬导线做成一边长为
的方框。将方框固定于纸面内，其右半部位于磁场区域中。求：
（1）导线中感应电流的大小；
（2）磁场对方框作用力的大小随时间的变化率。