如图所示，竖直平面坐标系xOy的第一象限，有垂直xOy面向外的水平匀强磁场和竖直向上的匀强电场，大小分别为B和E；第四象限有垂直xOy面向里的水平匀强电场，大小也为E；第三象限内有一绝缘光滑竖直放置的半径为R的半圆轨道，轨道最高点与坐标原点O相切，最低点与绝缘光滑水平面相切于N。一质量为m的带电小球从y轴上（y＞0）的P点沿x轴正方向进入第一象限后做圆周运动，恰好通过坐标原点O，且水平切入半圆轨道并沿轨道内侧运动，过N点水平进入第四象限，并在电场中运动（已知重力加速度为g）。
（1）判断小球的带电性质并求出其所带电荷量；
（2）P点距坐标原点O至少多高；
（3）若该小球以满足（2）中OP最小值的位置和对应速度进入第一象限，通过N点开始计时，经时间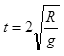
小球距N点的距离s为多远。
(10分)“辽宁号”航母在某次海试中，歼15舰载机降落着舰后顺利勾上拦阻索，在甲板上滑行s=117m停下。设舰载机勾上拦阻索后的运动可视为做匀减速直线运动，航母始终保持静止。已知飞机的质量m="3" x104kg，勾上拦阻索时的速度大小V0=78m／s，求：
(1)舰载机勾上拦阻索后滑行的时间t；
(2)舰载机滑行过程所受的总阻力f。
如图所示，用不可伸长的轻绳AC和BC吊起一质量不计的沙袋，绳AC和BC与天花板的夹角分别为60°和30°。现缓慢往沙袋中注入沙子。重力加速度g取10m/s2。
（1）当注入沙袋中沙子的质量m=10kg时，求绳AC和BC上的拉力大小FAC和FBC。
（2）若AC能承受的最大拉力为150N，BC能承受的最大拉力为100N，为使绳子不断
裂，求注入沙袋中沙子质量的最大值M。
一辆汽车由静止开始，在水平路面上做匀加速直线运动，加速度
。求：
（1）汽车在第5s末的速度大小v；
（2）汽车在前5s内的位移大小x。
某同学设计了一个测量长距离电动扶梯加速度的实验，实验装置如图1所示。将一电子健康秤置于水平的扶梯台阶上，实验员站在健康秤上相对健康秤静止。使电动扶梯由静止开始斜向上运动，整个运动过程可分为三个阶段，先加速、再匀速、最终减速停下。已知电动扶梯与水平方向夹角为37°。重力加速g取10m/s2，sin37°=0.6，cos37°=0.8。某次测量的三个阶段中电子健康秤的示数F随时间t的变化关系，如图2所示。
（1）画出加速过程中实验员的受力示意图；
（2）求该次测量中实验员的质量m；
（3）求该次测量中电动扶梯加速过程的加速度大小a1和减速过程的加速度大小a2。
如图所示，质量为M=1kg的长木板静止在光滑水平面上，现有一质量m=0.5kg的小滑块（可视为质点）以v0=3m/s的初速度从左端沿木板上表面冲上木板，带动木板一起向前滑动。已知滑块与木板间的动摩擦因数
，重力加速度g取10m/s2。求：
（1）滑块在木板上滑动过程中，长木板受到的摩擦力大小f和方向；
（2）滑块在木板上滑动过程中，滑块相对于地面的加速度大小a；
（3）滑块与木板A达到的共同速度v。