如图所示,水平轻弹簧左端固定在竖直墙上,右端被一用轻质细线拴住的质量为m的光滑小球压缩(小球与弹簧未拴接)。小球静止时离地高度为h。若将细线烧断,则(取重力加速度为g,空气阻力不计)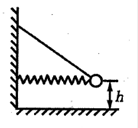
| A.小球立即做平抛运动 |
| B.细线烧断瞬间小球的加速度为重力加速度g |
| C.小球脱离弹簧后做匀变速运动 |
D.小球落地时重力瞬时功率等于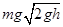 |
某同学用易得的材料制作了一个简易的实验仪器,如图所示.它可以用来()
| A.测电流 | B.测电阻 |
| C.测电容 | D.检验物体是否带电 |
如图所示的点是云南民族中学某同学在做“研究小车运动”实验时打下的点,按打点的刻的顺序分别取O、A、B、C、D为计数点,所用的电源频率是50Hz.下列关于结论中正确的是()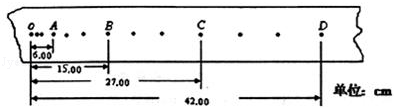
A.vA=1.25m/s,a=8.33m/s2
B.vA=1.50m/s,a=3.00m/s2
C.由图中数据可知小车做匀减速直线运动
D.由图中数据可知小车做匀加速直线运动
在探究一根轻质弹簧的弹力和伸长的关系的实验中,根据测量数据作出了弹力F和弹簧的形变量x的关系图象.下列说法正确的是()
| A.图线是经过坐标原点的曲线,说明F与x成正比 |
| B.图线是经过坐标原点的直线,说明F与x成正比 |
| C.弹簧的劲度系数与弹力成正比 |
| D.图线的斜率就是弹簧的劲度系数 |
一本书放在水平桌面上,下列说法正确的是()
| A.桌面受到的压力实际就是书的重力 |
| B.桌面受到的压力是由桌面形变形成的 |
| C.桌面对书的支持力与书的重力是一对平衡力 |
| D.桌面对书的支持力与书对桌面的压力一定大小相等,而且为同一性质的力 |
两个物体相互接触,关于接触处的弹力和摩擦力,以下说法正确的是()
| A.一定有弹力,但不一定有摩擦力 |
| B.如果有弹力,则一定有摩擦力 |
| C.如果有摩擦力,则一定有弹力 |
| D.如果有摩擦力,则其大小一定与弹力成正比 |