已知抛物线y=x²-4x+3．
（1）该抛物线的对称轴是        ，顶点坐标                ；
（2）将该抛物线向上平移2个单位长度，再向左平移3个单位长度得到新的二次函数图像，请写出相应的解析式，并用列表，描点，连线的方法画出新二次函数的图像；

x	…						…
y	…						…

 

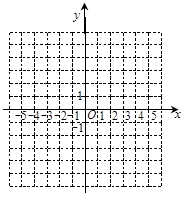
（3）新图像上两点A（x₁，y₁），B（x₂，y₂），它们的横坐标满足＜-2，且-1＜＜0，试比较y₁，y₂，0三者的大小关系．

科目 数学   题型 解答题   难度 中等

知识点： 二次函数在给定区间上的最值