如图,在等边△ABC中,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.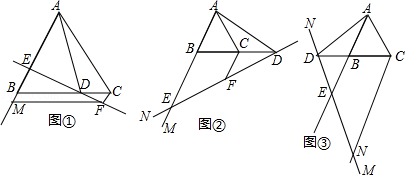
(1)当点D在线段BC上,∠NDB为锐角时,如图①,求证:CF+BE=CD;
(提示:过点F作FM∥BC交射线AB于点M.)
(2)当点D在线段BC的延长线上,∠NDB为锐角时,如图②;当点D在线段CB的延长线上,∠NDB为钝角时,如图③,请分别写出线段CF,BE,CD之间的数量关系,不需要证明;
(3)在(2)的条件下,若∠ADC=30°,S△ABC=4 ,则BE= ,CD= .
,则BE= ,CD= .
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图,请结合图象信息解答下列问题: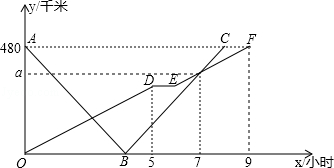
(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)两车出发后几小时相距的路程为200千米?请直接写出答案.
某校为了了解本校九年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对九年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中不近视与重度近视人数的和是中度近视人数的2倍.
请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图,在扇形统计图中,“不近视”对应扇形的圆心角度数是 144 度;
(3)若该校九年级学生有1050人,请你估计该校九年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人.
在△ABC中,AB=AC=5,BC=6,以AC为一边作正方形ACDE,过点D作DF⊥BC交直线BC于点F,连接AF,请你画出图形,直接写出AF的长,并画出体现解法的辅助线.
如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣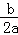 ,
, ).
).