如图所示,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点。
(Ⅰ)求证:平面FGH⊥平面AEB;
(Ⅱ)在线段PC上是否存在一点M,使PB⊥平面EFM?若存在,求出线段PM的长;若不存在,请说明理由.
(本题满分15分) 如图所示,在等腰梯形 中,
中,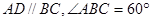 ,
, ,
, 为
为 中点.将
中点.将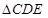 沿
沿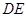 折起至
折起至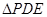 ,使得平面
,使得平面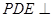 平面
平面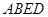 ,
,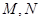 分别为
分别为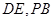 的中点.
的中点.
(Ⅰ) 求证: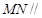 面
面 ;
;
(Ⅱ) 求二面角 的余弦值.
的余弦值.
(本题满分14分) 已知等差数列 的公差
的公差 大于
大于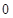 ,且
,且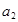 、
、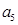 是方程
是方程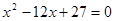 的两根.数列
的两根.数列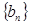 的前
的前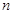 项和为
项和为 ,满足
,满足
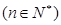

(Ⅰ) 求数列 ,
,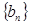 的通项公式;
的通项公式;
(Ⅱ) 设数列 的前
的前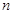 项和为
项和为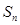 ,记
,记 .若
.若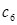 为数列
为数列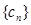 中的最大项,求实数
中的最大项,求实数 的取值范围.
的取值范围.
(本题满分14分) 在△ABC中,角A,B,C所对的边分别为a,b,c,且 .
.
(Ⅰ) 求 的值;
的值;
(Ⅱ) 当 ,
,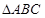 的面积
的面积 时,求
时,求 的值.
的值.
已知a,b是实数,函数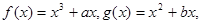
 和
和 是
是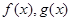 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称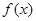 和
和 在区间
在区间 上单调性一致
上单调性一致
(1)设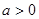 ,若
,若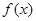 和
和 在区间
在区间 上单调性一致,求b的取值范围;
上单调性一致,求b的取值范围;
(2)设 且
且 ,若
,若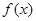 和
和 在以a,b为端点的开区间上单调性一致,求|a―b|的最大值
在以a,b为端点的开区间上单调性一致,求|a―b|的最大值
已知函数 在R上有定义,对任何实数
在R上有定义,对任何实数 和任何实数
和任何实数 ,都有
,都有
(Ⅰ )证明
)证明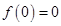 ;
;
(Ⅱ)证明 其中
其中 和
和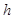 均为
均为 常数;
常数;
(Ⅲ)当(Ⅱ)中的 时,设
时,设 ,讨论
,讨论 在
在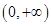 内的单调性并求极值。
内的单调性并求极值。