操作与探究
我们知道:过任意一个三角形的三个顶点能作一个圆,探究过四边形四个顶点作圆的条件。
(1)分别测量下面各四边形的内角,如果过某个四边形的四个顶点能一个圆,那么其相对的两个角之间有什么关系?证明你的发现.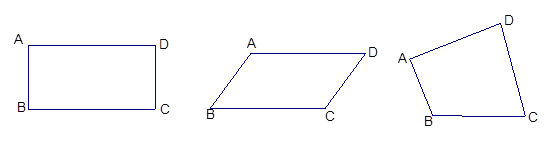
(2) 如果过某个四边形的四个顶点不能一个圆,那么其相对的两个角之间有上面的关系吗?试结合下面的两个图说明其中的道理.(提示:考虑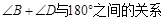 )
)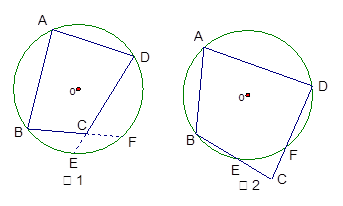
由上面的探究,试归纳出判定过四边形的四个顶点能作一个圆的条件.
如图,AB,CD是⊙O的直径,点E在AB延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD延长线于点G,DG=GE=3,连接FD.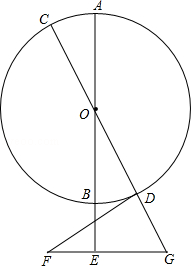
(1)求⊙O的半径;
(2)求证:DF是⊙O的切线.
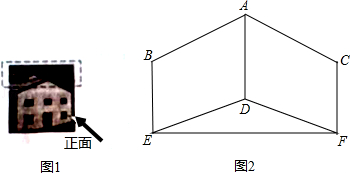
如图,图1是某仓库的实物图片,图2是该仓库屋顶(虚线部分)的正面示意图,BE、CF关于AD轴对称,且AD、BE、CF都与EF垂直,AD=3米,在B点测得A点的仰角为30°,在E点测得D点的仰角为20°,EF=6米,求BE的长.
(结果精确到0.1米,参考数据: )
)
为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.请根据图表中提供的信息,解答下列问题: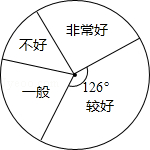
| 整理情况 |
频数 |
频率 |
| 非常好 |
0.21 |
|
| 较好 |
70 |
|
| 一般 |
||
| 不好 |
36 |
(1)本次抽样共调查了多少学生?
(2)补全统计表中所缺的数据.
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
如图,点A(1,a)在反比例函数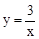 (x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数
(x>0)的图象上,AB垂直于x轴,垂足为点B,将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,点D落在反比例函数 (x>0)的图象上.
(x>0)的图象上.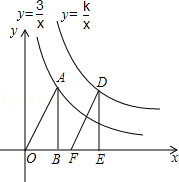
(1)求点A的坐标;
(2)求k值.
先化简,再求值: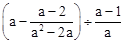 ,其中
,其中 .
.