李经理在某地以10元/千克的批发价收购了2 000千克核桃，并借一仓库储存．在存放过程中，平均每天有6千克的核桃损耗掉，而且仓库允许存放时间最多为60天．若核桃的市场价格在批发价的基础上每天每千克上涨0.5元。
（1）存放x天后，将这批核桃一次性出售，如果这批核桃的销售总金额为y元，试求出y与x之间的函数关系式；
（2）如果仓库存放这批核桃每天需要支出各种费用合计340元，李经理要想获得利润22 500元，需将这批核桃存放多少天后出售？（利润＝销售总金额－收购成本－各种费用）
(满分l0分)如图，△ABC是等边三角形，点D是AC的中点，延长BC到点E，使CE=CD．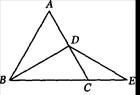
(1)用尺规作图的方法，过点D作DM⊥BE，垂足为M(不写作法，保留作图痕迹)；
(2)求证：BM=EM．
(每小题8分，共16分)
(1)计算：︱-2︱+2sin30°-(-
)2+(tan45°)-1；
(2)先化简，再求值：
，其中a=tan60°-l．
(每小题7分，共14分)
(1)解方程：x2—6x+1=0；
(2)解方程：
=
．
(满分l6分)如图5—9，已知点O为坐标原点，∠AOB=30°，∠ABO=90°，且点A的坐标为(2，0)。
(1)求点B的坐标；
(2)若二次函数y=ax2+bx+c的图象经过A，B，O三点，求此二次函数的解析式；
(3)在(2)中的二次函数图象的OB段(不包括点O，B)上，是否存在一点C，使得四边形ABCO的面积最大?若存在，求出这个最大值及此时点C的坐标；若不存在，请说明理由。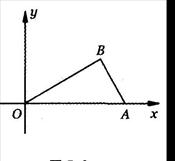
(满分l4分)如图，已知AB为⊙O的直径，弦CD⊥AB，垂足为点H．
(1)求证：AH·AB=AC2；
(2)若过点A的直线与弦CD(不含端点)相交于点E，与⊙O相交于点F，求证：AE·AF=AC2；
(3)若过点A的直线与直线CD相交于点P，与⊙O相交于点Q，判断AP·AQ=AC2是否成立(不必证明)．