小明对直角三角形很感兴趣. △ABC中,∠ACB=90°,D是AB上任意一点,连接DC,作DE⊥DC,EA⊥AC,DE与AE交于点E.请你跟着他一起解决下列问题: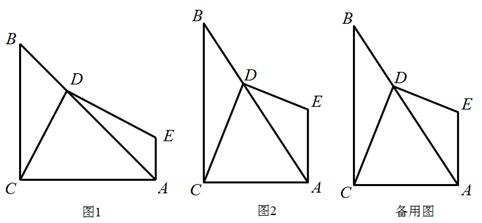
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE, DC有什么数量关系?请给出证明.
(·湖北黄冈,22题,分)(8 分)如图,反比例函数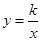 的图象经过点A(
的图象经过点A(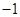 ,4),直线
,4),直线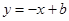 (
(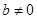 )与双曲线
)与双曲线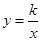 在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.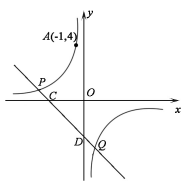
(1)求k 的值;
(2)当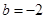 时,求△OCD 的面积;
时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得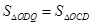 ? 若存在,请求出b 的值;若不存在,请说明理由.
? 若存在,请求出b 的值;若不存在,请说明理由.
(·湖北衡阳,27题,分)(本小题满分10分)如图,顶点M在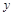 轴上的抛物线与直线
轴上的抛物线与直线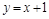 相交于A、B两点,且点A在
相交于A、B两点,且点A在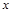 轴上,点B的横坐标为2,连结AM、BM.
轴上,点B的横坐标为2,连结AM、BM.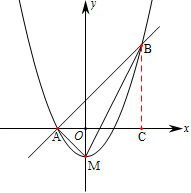
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线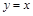 的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(
的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(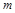 ,
,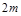 ),当
),当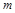 满足什么条件时,平移后的抛物线总有不动点?
满足什么条件时,平移后的抛物线总有不动点?
(·湖北衡阳,25题,分)(本小题满分8分)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物深度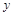 (微克/毫升)与服药时间
(微克/毫升)与服药时间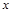 小时之间的函数关系如图所示(当
小时之间的函数关系如图所示(当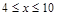 时,
时,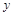 与
与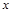 成反比).
成反比).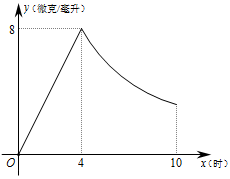
(1)根据图象分别求出血液中药物浓度上升和下降阶段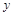 与
与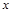 之间的函数关系式;
之间的函数关系式;
(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?
(·湖北武汉,20题,分)(本题8分)如图,已知点A(-4,2)B(-1,-2),□ABCD的对角线交于坐标原点O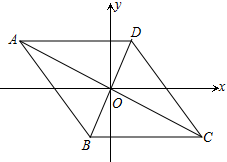
(1)请直接写出点C、D的坐标
(2)写出从线段AB到线段CD的变换过程
(3)直接写出□ABCD的面积
(·湖南益阳)已知点P是线段AB上与点A不重合的一点,且AP<PB.AP绕点A逆时针旋转角α(0°<α≤90°)得到AP1,BP绕点B顺时针也旋转角α得到BP2,连接PP1、PP2.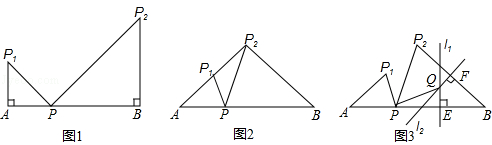
(1)如图1,当α=90°时,求∠P1PP2的度数;
(2)如图2,当点P2在AP1的延长线上时,求证:△P2P1P∽△P2PA;
(3)如图3,过BP的中点E作l1⊥BP,过BP2的中点F作l2⊥BP2,l1与l2交于点Q,连接PQ,求证:P1P⊥PQ.