为了预防流感,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例,药物燃烧后,y与x成反比例（如图）,现测药物8分钟燃毕,此时空气中每立方米含药量为6毫克,请根据题中所提供的信息,回答下列问题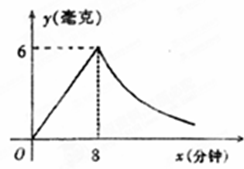
（1）药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范围是 ;药物燃烧完后,y与x的函数关系式为
（2）研究表明,当空气中的每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室.
（3）研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效地杀灭空气中的病菌,那么此次消毒是否有效？为什么？
在直角坐标系中，有以 为顶点的正方形，设它在折线 上侧部分的面积为 ，求 关于 的函数关系式.
编号为 到 的 个弹珠被分别放在两个篮子 和 中， 号弹珠在篮子 中，把这个弹珠从篮子 移至篮子 中，这时篮子 中的弹珠号码数的平均数等于原平均数加 篮中弹珠号码数的平均数也等于原平均数加 ，问原来在篮子 中有多少个弹珠?
我国是水资源比较贫乏的国家之一，各地采用了价格调控等手段来达到节约用水的目的.某市用水收费的方法是：水费 基本费十超额费十定额损耗费.若每月用水量不超过最低限量 时，只付基本费 元和每月的定额损耗费 元；若用水量超过 时，除了付同上的基本费和定额损耗费外，超过部分每立方米付 元的超额费.已知每户每月的定额损耗费不超过 元.
（1）当月用水量为 时，支付费用为 元，写出 关于 的函数关系式；
（2）该市一家庭今年一季度的用水量和支付费用见下表，根据表中数据求 .
如图，在四边形 中， .点 从点 出发，以 的速度向 点运动；点 从点 同时出发，以 的速度向点 运动，规定其中一个动点到达端点时，另一个动点也随之停止运动.设运动时间为 .
（1） 为何值时，四边形 是矩形?
（2） 为何值时，四边形 是平行四边形?
（3）在其它条件不变的情况下，能否通过改变点 的运动速度，使得四边形 是菱形?
设 为自然数，如果 成立，求 的值.