提出问题:如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?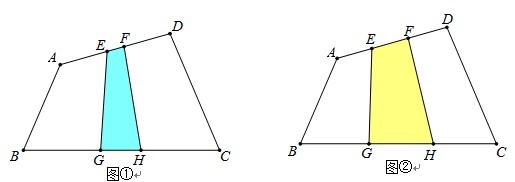
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1)如图②:四边形ABCD中,点E、F是AD的3等分点,点G、H是BC的3等分点,连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?
如图③,连接EH、BE、DH,
因为△EGH与△EBH高相等,底的比是1:2,
所以S△EGH=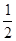 S△EBH
S△EBH
因为△EFH与△DEH高相等,底的比是1:2,
所以S△EFH=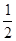 S△DEH
S△DEH
所以S△EGH+S△EFH=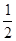 S△EBH +
S△EBH +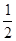 S△DEH
S△DEH
即S四边形EFHG=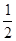 S四边形EBHD
S四边形EBHD
连接BD,
因为△DBE与△ABD高相等,底的比是2:3,
所以S△DBE= S△ABD
S△ABD
因为△BDH与△BCD高相等,底的比是2:3,
所以S△BDH= S△BCD
S△BCD
所以S△DBE +S△BDH= S△ABD+
S△ABD+ S△BCD =
S△BCD = (S△ABD+S△BCD)
(S△ABD+S△BCD)
= S四边形ABCD
S四边形ABCD
即S四边形EBHD=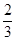 S四边形ABCD
S四边形ABCD
所以S四边形EFHG=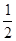 S四边形EBHD=
S四边形EBHD=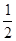 ×
×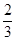 S四边形ABCD=
S四边形ABCD=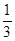 S四边形ABCD
S四边形ABCD
(1)如图④:四边形ABCD中,点E、F是AD的5等分点中最中间2个,点G、H是BC的5等分点中最中间2个,连接EG、FH,猜想:S四边形EFHG与S四边形ABCD之间有什么关系呢
验证你的猜想:
(2)问题解决:如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,连接EG、FH,(其中n为奇数)
那么S四边形EFHG与S四边形ABCD之间的关系为: (不必写出求解过程)
多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示。可是她忘记了在图中标出原点和x轴、y轴。只知道马场的坐标为(-3,-3),你能帮她建立平面直角坐标系并求出其他各景点的坐标?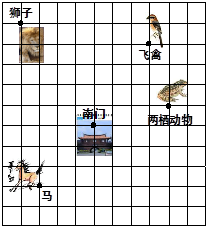
解下列方程组
(1)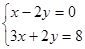 (2)
(2)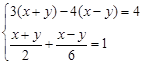
化简:
已知,在平面直角坐标系中,A(a,0)、B(0,b),a、b满足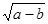 +|a−3
+|a−3 |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
|=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)求∠OAB的度数;
(2)设AB=6,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;
(3)设AB=6,若∠OPD=45°,求点D的坐标.
如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.