已知直线
分别与y轴、x轴相交于A、B两点，与二次函数
的图像交于A、C两点．
(1)当点C坐标为（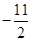
，
）时，求直线AB的解析式；
(2)在（1）中，如图，将△ABO沿y轴翻折180°，若点B的对应点D恰好落在二次函数的图像上，求点D到直线AB的距离；
(3)当-1≤x≤1时，二次函数有最小值-3,求实数m的值.
已知：如图，锐角△ABC的两条高BD、CE相交于点O，且OB=OC．试说明△ABC是等腰三角形．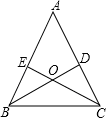
如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．求证：BC∥EF．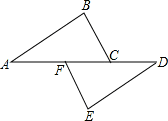
画图：牧童在A处放牛，其家在B处，若牧童从A处将牛牵到河边C处饮水后再回家，试问C在何处，所走路程最短？（保留作图痕迹）
某地电话拨号上网有两种收费方式，用户可以任选一种。
A、计时制，每分钟0.05元；
B、包月制：每月50元（限一部个人住宅电话上网）。
此外，每种上网方式都要增收每分钟0.02元的通讯费
（1）某用户某月上网时间为x小时，请用代数式表示两种收费方式下，该用户分别应支付的费用。
A:B:
（2）若某用户估计每月上网时间为20小时，通过计算说明应该采用哪一种付费方式较为合算。
若“△”表示一种新运算，规定a△b=a×b-（a+b），请计算下列各式的值
（1）-3△5（2）2△[（-4）△（-5）]