如图,在平面直角坐标系中,已知抛物线 交
交 轴于A(2,0),B(6,0)两点,交
轴于A(2,0),B(6,0)两点,交 轴于点C(0,
轴于点C(0, ).
).
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交 轴于点E、F两点,求劣弧EF所对圆心角的度数;
轴于点E、F两点,求劣弧EF所对圆心角的度数;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
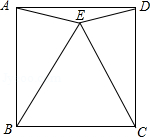
如图,四边形 是正方形, 是等边三角形.
(1)求证: ;
(2)求 的度数.
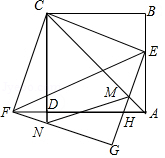
如图,正方形 的边长为1,点 为边 上一动点,连接 并将其绕点 顺时针旋转 得到 ,连接 ,以 、 为邻边作矩形 , 与 、 分别交于点 、 , 交 延长线于点 .
(1)证明:点 、 、 在同一条直线上;
(2)随着点 的移动,线段 是否有最小值?若有,求出最小值;若没有,请说明理由;
(3)连接 、 ,当 时,求 的长.
如图, 的顶点 、 分别在 轴, 轴上, ,且 的面积为8.
(1)直接写出 、 两点的坐标;
(2)过点 、 的抛物线 与 轴的另一个交点为点 .
①若 是以 为腰的等腰三角形,求此时抛物线的解析式;
②将抛物线 向下平移4个单位后,恰好与直线 只有一个交点 ,求点 的坐标.

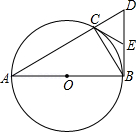
如图,已知 内接于 , 为 的直径, ,交 的延长线于点 .
(1) 为 的中点,连接 ,求证: 是 的切线;
(2)若 ,求 的大小.
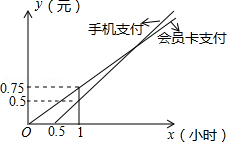
为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额 (元 与骑行时间 (时 之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额 (元 与骑行时间 (时 的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.