在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.
(1)求b的值和点D的坐标;
(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
(3)在(2)的条件下,如果以PD为半径的圆P与圆O外切,求圆O的半径.
如图,在Rt△ABC中,∠C=90°,以BC为直径作⊙O交AB于点D,取AC的中点E,连结DE、OE.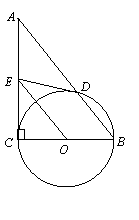
(1)求证:DE是⊙O的切线;(2)如果⊙O的半径是1.5cm,ED=2cm,求AB的长.
小晶和小红玩掷骰子游戏,每人将一个各面分别标有1,2,3,4,5,6的正方体骰子掷一次,把两人掷得的点数相加,并约定:点数之和等于6,小晶赢;点数之和等于7.小红赢;点数之和是其它数,两人不分胜负.问他们两人谁获胜的概率大?请你用“画树状图”或“列表”的方法加以分析说明.
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.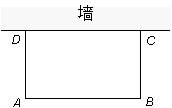
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2,为什么?
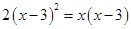 .
.
 (用配方法).
(用配方法).