已知函数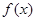 是定义在R上的奇函数,
是定义在R上的奇函数,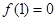 ,当
,当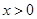 时,
时,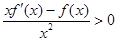 ,则不等式
,则不等式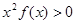 的解集是______________
的解集是______________
将一骰子(六个面标有1—6个圆点的正方体)抛掷两次,所得向上点数分别为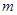 和
和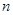 ,则函数
,则函数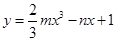 在
在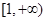 上为增函数的概率是__________(结果用分数表示).
上为增函数的概率是__________(结果用分数表示).
有下列命题
①命题“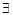 x∈R,使得
x∈R,使得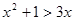 ”的否定是“
”的否定是“ 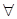 x∈R,都有
x∈R,都有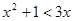 ”;
”;
②设p、q为简单命题,若“p∨q”为假命题,则“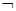 p∧
p∧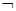 q为真命题”;
q为真命题”;
③“a>2”是“a>5”的充分不必要条件;
④若函数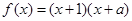 为偶函数,则
为偶函数,则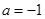 ;
;
其中所有正确的说法序号是
给出下面的数表序列: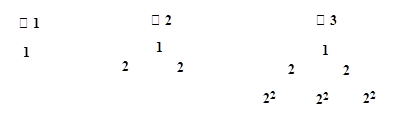
其中表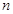 (
(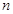 ="1,2,3"
="1,2,3" 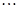 )有
)有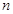 行,表中每一个数“两脚”的两数都是此数的2倍,记表
行,表中每一个数“两脚”的两数都是此数的2倍,记表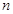 中所有的数之和为
中所有的数之和为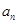 ,例如
,例如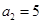 ,
,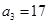 ,
,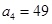 .则
.则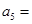 .
.
函数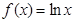 在
在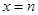
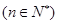 处的切线斜率为
处的切线斜率为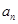 ,
,
则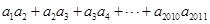 =.
=.