如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动.设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为

在 中,
中,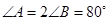 ,则
,则 等于
等于
| A.40° | B.60° |
C.80° | D.120° |
据报道,2011年北京市户籍人口中,60岁以上的老人有2460000人,预计未来五年北京人口“老龄化”还将提速.将2460000用科学记数法表示为
| A.0.25×106 | B.24.6×105 | C.2.46×105 | D.2.46×106 |
 的相反数是
的相反数是
A. |
B. |
C.2 | D.-2 |
如图,反比例函数y= (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E。若四边形ODBE的面积为12,则k的值为()
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E。若四边形ODBE的面积为12,则k的值为()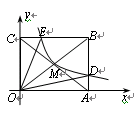
A. 1B. 2C.3D. 4
如图,在平行四边形ABCD中,O1、O2、O3分别是对角线BD上的三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于点F,则AD:DF等于()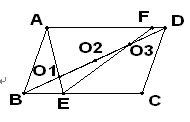
| A.19:2 | B.9:1 | C.8:1 | D.7:1 |