如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A（4,4）,B（1,3）,C（3,3）,D（3,1）.
（1）画出“基本图形”关于原点O对称的四边形A1B1C1D1,并求出A1,B1,C1,D1的坐标.
A1( , ),B1( , ),C1( , ),D1( , ) ;
（2）画出“基本图形”关于x轴的对称图形A2B2C2D2 ;
（3）画出四边形A3B3C3D3,使之与前面三个图形组成的图形既是中心对称图形又是轴对称图形.
解不等式组
计算：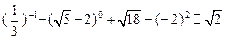
如图，已知∠ACB＝90°，AC＝BC，BE⊥CE于E，AD⊥CE于D，CE与AB相交于F．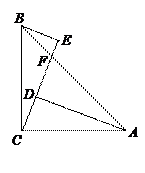
（1）求证：△CEB≌△ADC；
（2）若AD＝9cm，DE＝6 cm，求BE的长．
(10分) 如图①，一个无盖的正方体盒子的棱长为6厘米，顶点C1处有一只昆虫甲，在盒子的内部顶点A处有一只昆虫乙．（盒壁的厚度忽略不计）
（1）假设昆虫甲在顶点C1处静止不动，如图①，在盒子的内部我们先取棱BB1的中点E，再连结AE、EC1．昆虫乙如果沿路径A→E→Cl 爬行 , 那么可以在最短的时间内捕捉到昆虫甲．仔细体会其中的道理，并在图①中画出另一条路径，使昆虫乙从顶点A沿这条路径爬行，同样可以在最短的时间内捕捉到昆虫甲．（请简要说明画法）
（2）如图②，假设昆虫甲从顶点C1以1厘米/秒的速度沿盒子的棱C1D1向D1爬行，同时昆虫乙从顶点A以2.5厘米/秒的速度在盒壁上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？
(10分) 如图，Rt△ABC中，∠C = 90°，把Rt△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB上．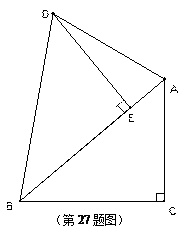
（1）若∠BDA = 70°，求∠BAC的度数．
（2）若BC = 8，AC = 6，求△ABD中AD边上的高．