如图,已知抛物线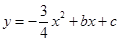 与坐标轴交于
与坐标轴交于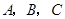 三点,点
三点,点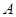 的横坐标为
的横坐标为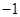 ,过点
,过点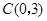 的直线
的直线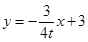 与
与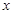 轴交于点
轴交于点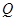 ,点
,点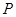 是线段
是线段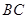 上的一个动点,
上的一个动点,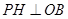 于点
于点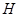 .若
.若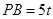 ,且
,且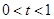 .
.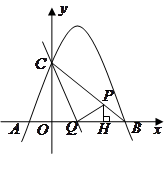
(1)求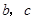 的值
的值
(2)求出点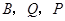 的坐标(其中
的坐标(其中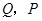 用含
用含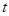 的式子表示):
的式子表示):
(3)依点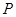 的变化,是否存在
的变化,是否存在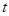 的值,使
的值,使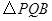 为等腰三角形?
为等腰三角形?
已知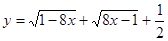 ,求代数式
,求代数式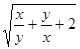 的值.
的值.
先化简再求值:当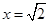 时,求代数式
时,求代数式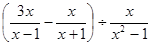 的值.
的值.
解方程 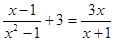
如图,P1是 反比例函数
反比例函数 在第一象限图像上的一点,点A1的坐标为(2,0).
在第一象限图像上的一点,点A1的坐标为(2,0).
(1)当点P1的横坐标逐渐增大时,△P1O A1的面积
将如何变化?
(2)若△P1O A1与△P2 A1 A2均为等边三角形,求
此反比例函数的解析式及A2点的坐标.
小莉的爸 爸买了今年七月份去上海看世博会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,
爸买了今年七月份去上海看世博会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,
将数字为1,2,3,5的四张牌给小莉,将数字为4,6,7,8的四张牌留给自己,并
按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两
张扑克牌数字相加,如果和 为偶数,则小莉去;如果和为奇数,则哥哥去.
为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)请用数状图或列表的方法求小莉去上海看世博会的概率;
(2)哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公
平的游戏规则.