如图1,某超市从一楼到二楼的电梯AB的长为16.50米,坡角∠BAC为32°.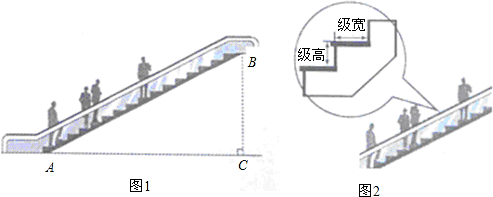
(1)求一楼与二楼之间的高度BC(精确到0.01米);
(2)电梯每级的水平级宽均是0.25米,如图2.小明跨上电梯时,该电梯以每秒上升2级的高度运行,10秒后他上升了多少米?(精确到0.01米)(备用数据:sin32°=0.5299,con32°=0.8480tan32°=0.6249。)
某型号汽车油箱的最大贮油量为60L,在正常情况下,每行驶50km耗油5.5L.
(1)在加满油的情况下,该车正常行驶x km后,油箱内还剩的油量是多少?
(2)试通过计算判断,在加满油的情况下,若该车要正常行驶到550km外的某地,中途是否需要再加油?
如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的三视图;
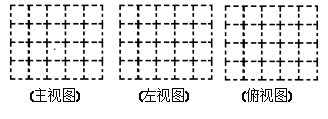
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
邮递员骑车从邮局出发,先向西骑行3km到达A村,继续向西骑行2km到达B村,然后向东骑行7km到达C村,再继续向东骑行3km到达D村,最后骑回邮局.
(1)C村离A村有多远?
(2)邮递员一共骑行了多少千米?
在数轴上把下列各数表示出来,并用“<”连接各数, ,1
,1 ,0,
,0, ,-(+1),4
,-(+1),4
观察下列等式: ,
, ,
, ,
,
将以上三个等式两边分别相加得: .
.
(1)猜想并写出:
(2)直接写出下列各式的计算结果: _____
_____
(3)探究并利用以上规律计算: