在坐标平面内,半径为R的⊙C与x轴交于点D(1,0)、E(5,0),与y轴的正半轴相切于点A。点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线BP,作EH⊥BP于H。
⑴求圆心C的坐标及半径R的值;
⑵△POB和△PHE随点P的运动而变化,若它们全等,求a的值;
⑶当a=6时,试确定直线BP与⊙C的位置关系并说明理由。
如图,△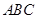 中,
中,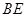 是它的角平分线,
是它的角平分线,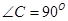 ,
,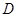 在
在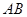 边上,以
边上,以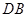 为直径的半圆
为直径的半圆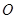 经过点
经过点 ,交
,交 于点
于点 。
。
(1)求证: 是
是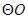 的切线;
的切线;
(2)若 ,连接
,连接 ,求证:
,求证: ∥
∥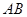 ;
;
(3)在(2)的条件下,若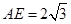 ,求图中阴影部分的面积。
,求图中阴影部分的面积。
如图,在边长为1个单位长度的小正方形组成的网格中, 的顶点A、B、C在小正方形的顶点上.将
的顶点A、B、C在小正方形的顶点上.将 向下平移4个单位、再向右平移3个单位得到△
向下平移4个单位、再向右平移3个单位得到△ ,然后将△
,然后将△ 绕点
绕点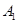 顺时针旋转90°得到△
顺时针旋转90°得到△ .
.
(1)在网格中画出△ 和△
和△ ;
;
(2)计算点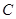 在变换到点
在变换到点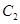 的过程中经过的路线长;
的过程中经过的路线长;
(3)计算线段 在变换到线段
在变换到线段 的过程中扫过的图形的面积.
的过程中扫过的图形的面积.
如图所示,在梯形 中,
中, ∥
∥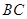 ,
,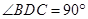 ,
,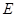 为
为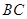 上一点,
上一点, .
.
(1)求证: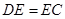 ;
;
(2)若 ,试判断四边形
,试判断四边形 的形状,并说明理由.
的形状,并说明理由.
已知关于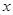 的一元二次方程
的一元二次方程 .
.
(1)试说明无论 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根;
(2)已知等腰 的底边
的底边 ,若两腰
,若两腰 、
、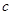 恰好是这个方程的两个根,求
恰好是这个方程的两个根,求 的周长.
的周长.
甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180;
(1)将下表填完整:
| 身高(厘米) |
176 |
177 |
178 |
179 |
180 |
| 甲队(人数) |
0 |
3 |
4 |
0 |
|
| 乙队(人数) |
2 |
1 |
1 |
(2)甲队队员身高的平均数为厘米,乙队队员身高的平均数为厘米;
(3)你认为哪支仪仗队身高更为整齐?请从方差的角度说明理由.