已知棱长为1的正方体ABCD
A1B1C1D1中, P,Q是面对角线A1C1上的两个不同动点.
①存在P,Q两点,使BP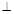
DQ;
②存在P,Q两点,使BP,DQ与直线B1C都成450的角;
③若|PQ|=1,则四面体BDPQ的体积一定是定值;
④若|PQ|=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值.
以上命题为真命题的个数是( )
| A．1 | B．2 | C．3 | D．4 |
已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是( )
| A．16π | B．20π | C．24π | D．32π |
三棱台ABC-A1B1C1中，AB∶A1B1=1∶2，则三棱锥A1—ABC，B—A1B1C，C—A1B1C1的体积之比为( )
| A．1∶1∶1 | B．1∶1∶2 | C．1∶2∶4 | D．1∶4∶4 |
在三棱锥A—BCD中，P、Q分别在棱AC、BD上，连结AQ、CQ、BP、PQ，若三棱锥A—BPQ，B—CPQ，C—DPQ的体积分别为6，2，8，则三棱锥A-BCD的体积为( )
A.20 B.24 C.28D.40
如图,在上、下底面对应边的比为1∶2的三棱台中，过上底面一边作一个平行于对棱的平面A1B1EF，这个平面分三棱台成两部分的体积之比为( )
| A．1∶2 | B．2∶3 | C．3∶4 | D．4∶5 |
两球的体积之和是12π，它们的大圆周长之和是6π，则两球的半径之差是( )
| A．1 | B．2 | C．3 | D．4 |