如图所示,有界匀强磁场区域的半径为r,磁场方向与导线环所在平面垂直,导线环半径也为r, 沿两圆的圆心连线方向从左侧开始匀速穿过磁场区域,在此过程中.关于导线环中的感应电流i随时间t的变化关系,下列图象中(以逆时针方向的电流为正)最符合实际的是( )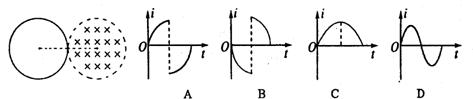
如图所示,AB是真空中点电荷形成的一条电场线,一个带正电的粒子只受电场力,以速度vA经过A点沿直线向B点运动,一段时间后,该粒子以相反的速度vB经过B点,则下列判断正确的是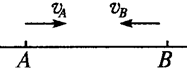
| A.A点的电势一定低于B点的电势 |
| B.A点的场强一定大于B点的场强 |
| C.该带电粒子在A点的电势能一定小于它在B点的电势能 |
| D.该带电粒子在A点时的动能与电势能之和小于它在B点时的动能与电势能之和 |
如图所示,周定的光滑倾斜杆上套有一个质量为m的圆环,圆环与竖直放置的轻质弹簧上端相连,弹簧的下端固定在水平地面上的A点,开始弹簧竖直并且长度恰好为原长h.现让圆环由静止沿杆滑下,滑到杆的底端(未触及地面)时速度恰好为零,已知当地的重力加速度大小为g.则在圆环下滑的整个过程中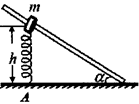
| A.圆环、弹簧和地球组成的系统机械能不守恒 |
| B.弹簧的弹性势能先增大后减小 |
| C.弹簧的弹性势能增大了mgh |
| D.弹簧的最大压缩量小于其最大伸长量 |
2011年8月12日,我国在西昌卫星发射中心,将巴基斯坦通信卫星1R(Paksat-1R)成功送入地球同步轨道,发射任务获得圆满成功.关于成功定点后的“1R”卫星,下列说法正确的是
| A.运行速度大于第一宇宙速度,小于第二宇宙速度 |
| B.离地面的高度根据需要可任意设定,相对地面保持静止 |
| C.绕地球运行的周期比月球绕地球运行的周期小 |
| D.向心加速度与静止在赤道上物体的向心加速度大小相等 |
一质量为m的小球,沿在竖直平面内的圆形轨道的内侧运动,经过轨道最高点而不脱离轨道的临界速度值是v.重力加速度为g,则当小球以2v的速度经过最高点时,对轨道的压力值是
| A.0 | B.mg | C.3mg | D.5mg |
一个倾角为θ(90°>θ>0°)的光滑斜面靠在竖直的光滑墙壁上,一铁球在一水平推力F作用下静止于墙壁与斜面之间,与斜面间的接触点为A,推力F的作用线通过球心,如图所示.则下列判断正确的是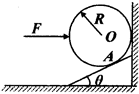
| A.墙面对球的弹力小于推力F |
| B.墙面对斜面的弹力与推力F大小相等 |
| C.斜面对球的支持力大于球的重力 |
| D.地面对斜面的支持力与球的重力大小相等 |