已知椭圆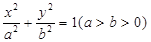 上的点
上的点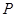 到左右两焦点
到左右两焦点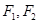 的距离之和为
的距离之和为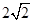 ,离心率为
,离心率为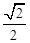 .
.
(1)求椭圆的方程;
(2)过右焦点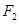 的直线
的直线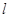 交椭圆于
交椭圆于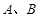 两点,若
两点,若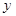 轴上一点
轴上一点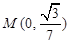 满足
满足 ,求直线
,求直线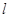 的斜率
的斜率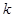 的值.
的值.
(本小题满分13分)
已知函数
(1)如果对任意 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)设实数 的两个极
的两个极 值点分别为
值点分别为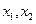 判断①
判断① ②
② ③
③ 是否为定值?若是定值请求出;若不是定值,请把不是定
是否为定值?若是定值请求出;若不是定值,请把不是定 值的表示为函数
值的表示为函数 并求出
并求出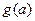 的最小值;
的最小值;
(3)对于(2)中的 设
设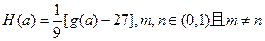 ,试比较
,试比较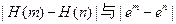 (e为自然对数的底)的大小,并证明。
(e为自然对数的底)的大小,并证明。
(本小题满分13分)已知双曲线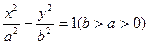 ,0为坐标原点,离心率
,0为坐标原点,离心率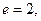
点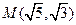 在双曲线上。
在双曲线上。
(1)求双曲线的方程;
(2)若直线l与双曲线交于P、Q两点,且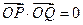 ,
,
求:|OP|2+|OQ|2的最小值。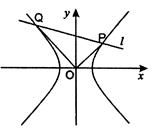
(本小题满分13分)在数列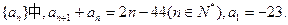
(1)求 ;(2)设
;(2)设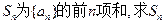 的最小值。
的最小值。
(本小题满分12分)已知矩形ABCD中,AB=6,BC=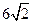 ,E为AD的中点(图一)。沿BE将△ABE折起,使二面角A—BE—C为直二面角(图二),且F为AC的中点。
,E为AD的中点(图一)。沿BE将△ABE折起,使二面角A—BE—C为直二面角(图二),且F为AC的中点。
(1)求证:FD//平面ABE;
(2)求二面角E-AB-C的余弦值。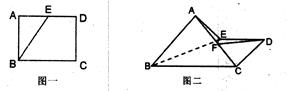
(本小题满分12分)从某小组的5名女生和4名男生中任选3人去参加一项公益活动。
(1)求 所选3人中恰有一名男生的概率;
所选3人中恰有一名男生的概率;
(2)求所选3人中男生人数ξ的分布列,并求ξ的期望。