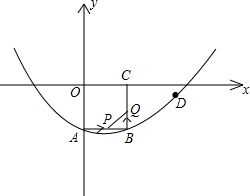
如图所示,在平面直角坐标系xoy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线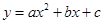
经过点A、B和D（4,
）．
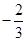（1）求抛物线的表达式．
（2）如果点P由点A出发沿AB边以2cm/s的速度向点B运动,同时点Q由点B出发,沿BC边以1cm/s的速度向点C运动,当其中一点到达终点时,另一点也随之停止运动．设S=PQ2（cm2）．
①试求出S与运动时间t之间的函数关系式,并写出t的取值范围;
②当S取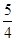
时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由．
（3）在抛物线的对称轴上求点M,使得M到D、A的距离之差最大,求出点M的坐标．
江南生态食品加工厂收购了一批质量为10000千克的某种山货，根据市场需求对其进行粗加工和精加工处理，已知精加工的该种山货质量比粗加工的质量3倍还多2000千克，求粗加工的该种山货质量．
依据下列解方程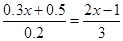
的过程，请在前面的括号内填写变形步骤，在后面的括号内填写变形依据。
解：原方程可变形为
( ______________________ )
去分母，得3（3x+5）=2(2x－1). ( ______________________ )
去括号，得9x+15=4x－2.（_________________________ ）
( ____________________ )，得9x－4x=－15－2. ( ______________________ )
合并，得5x=－17. ( 合并同类项)
（ ____________________ ），得x=
.（_________________________）
先化简，再求值：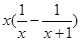
，其中
.
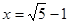先化简再求值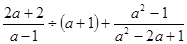
其中a=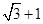
（2011山东东营，18（2），4分）先化简，再求值: 
,其中