设全集为 ,集合
,集合 ,
,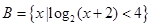 .
.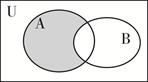
(1)求如图阴影部分表示的集合;
(2)已知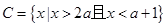 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且二面角A-DC-E为直二面角。
(1)求证:CD⊥DE;(2)求AE与面DEC所成的角.
(本小题满分12分)美国次贷危机引发全球金融动荡,波及中国沪深两大股市,甲、乙、丙3人打算趁股市低迷之际买入股票。三人商定在圈定的10只股票中各自随机购买1只(假定购买时,每只股票的基本情况完全相同)
(1)求甲、乙、丙3人恰好买到相同股票的概率;
(2)求甲、乙、丙3人中至少有2人买到相同股票的概率.
(本小题满分12分)
(1)已知 ,求
,求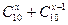 的值;
的值;
(2)若 的展开式中第3项为常数项,求
的展开式中第3项为常数项,求 .
.
(本小题满分10分)
四棱锥P-ABCD中,底面ABCD是正方形,
边长为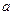 ,PD=
,PD=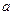 ,PD⊥平面ABCD
,PD⊥平面ABCD
(1)求证: AC⊥PB ;
(2)求二面角A-PB-D的大小;
(3)求四棱锥外接球的半径.
(4)在这个四棱锥中放入一个球,求球的最大半径;
(本小题共10分)
已知数列 满足:
满足: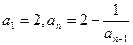 ,
, ,
,
(1)求证:数列 为等差数列; (2) 求数列
为等差数列; (2) 求数列 的通项公式;
的通项公式;
(3)令 ,求证:
,求证: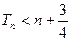 .
.