如图所示,圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v从A点沿直径AOB方向射入磁场,经过Δt时间从C点射出磁场,OC与OB成60°角。现将带电粒子的速度变为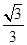 v,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为
v,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为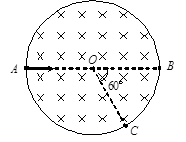
A.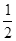 Δt Δt |
B.2Δt |
C. Δt Δt |
D. Δt Δt |
如图所示,三个相同的轻质弹簧连接在O点,弹簧1的另一端固定在天花板上,且与竖
直方向的夹角为30°,弹簧2水平且右端固定在竖直墙壁上,弹簧3的另一端悬挂质量
为m的物体且处于静止状态,此时弹簧1、2、3的形变量分别为x1、x2、x3,则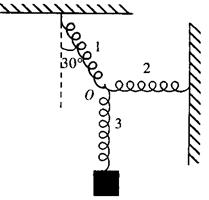
A.x1:x2:x3=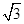 :1 :2 :1 :2 |
B.x1:x2:x3= 2 :1 :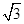 |
C.x1: x2:x3=1 :2 :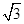 |
D.x1:x2:x3=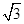 :2 :1 :2 :1 |
汽车在水平面上刹车,其位移与时间的关系是x=24t-6t2,则它在前3s内的平均速度为
| A.6 m/s | B.8 m/s | C.10 m/s | D.12 m/s |
酒后驾驶会使驾驶员的“反应时间”变长而增加安全隐患。“反应时间”指驾驶员发现情况到采取制动的时间;“反应距离”指驾驶员从发现前方出现危险情况到开始实施制动汽车行驶的距离;“制动停车距离”指驾驶员从看到危险情况到停车时的距离(假设汽车制动时的加速度大小都相同)。下表是某车驾驶测试实验的数据:
| 速度(m/s) |
反应距离/m |
制动停车距离/m |
||
| 正常 |
酒后 |
正常 |
酒后 |
|
| 10 |
8.0 |
25.0 |
14.3 |
31.3 |
| 15 |
12.0 |
37.5 |
26.1 |
51.6 |
| 20 |
16.0 |
50.0 |
41.0 |
x |
| 25 |
20.0 |
62.5 |
59.1 |
101.6 |
分析上述数据,下列说法正确的是
A.表中x为91.0
B.汽车制动时,加速度大小为12m/s2
C.驾驶员酒后反应时间比正常情况下多1s
D.若汽车以20m/s的速度行驶时,发现前方60m处有险情,酒后驾驶则不能安全停车
小球从空中自由下落,与水平地面相碰后弹到空中某一高度,其速度随时间变化的关系如图所示.取g="10" m/s2.则()
| A.小球下落的最大速度为5 m/s |
| B.小球第一次反弹初速度的大小为5 m/s |
| C.小球能弹起的最大高度为0.45 m |
| D.小球能弹起的最大高度为1.25 m |
某质点从t = 0开始由原点出发,其运动速度-时间图象如图所示,由图可判断
| A.t = 1s时,离原点最远 |
| B.第 1s 末速度改变方向,第2s末加速度为0 |
| C.t =" 2s" 时,离原点最远 |
| D.t =" 4s" 时,回到原点 |