如图所示,两根质量均为m、电阻均为R、长度均为l的导体棒a、b,用两条等长的、质量和电阻均可忽略的、不可伸长的柔软长直导线连接后,b放在距地面足够高的光滑绝缘水平桌面上,a靠在桌子的光滑绝缘侧面上;两根导体棒均与桌子边缘平行。整个空间存在水平向右的匀强磁场,磁感应强度为B。开始时两棒静止,自由释放后开始运动,导体棒a在落地前就已匀速运动,此时导体棒b仍未离开桌面。已知两条导线除桌边拐弯处外其余部位均处于伸直状态,导线与桌子侧棱间无摩擦。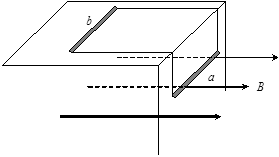
(1)试求导体棒匀速运动时的速度大小。
(2)从自由释放到刚匀速运动的过程中,若通过导体棒横截面的电荷量为q,求该过程中系统产生的焦耳热。
水上滑梯可简化成如图所示的模型,斜槽AB和水平槽BC平滑连接,斜槽AB的竖直高度H=6.0m,倾角θ=37°。水平槽BC长d=2.0m,BC面与水面的距离h=0.80m,人与AB、BC间的动摩擦因数均为μ=0.10。取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6。一小朋友从滑梯顶端A点无初速地自由滑下,求:
(1)小朋友沿斜槽AB下滑时加速度的大小a;
(2)小朋友滑到C点时速度的大小υ;
(3)在从C点滑出至落到水面的过程中,小朋友在水平方向位移的大小x。
如图所示,P、N是两个长为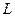 的平行板,它们相距
的平行板,它们相距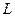 ,今有一个质量为
,今有一个质量为 、带电量为
、带电量为 的正电荷以速度
的正电荷以速度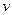 沿平行板面的方向贴着P板从一端打入。①如果板间加一个垂直于纸面向外的磁场后,该带电粒子可以打出平行板区域,试求磁场的磁感应强度B的取值范围;②如果板间加一个垂直于板面从P板指向N板的电场后,带电粒子可从板间射出,则所加电场的场强怎样取值?(带电粒子的重力不计)
沿平行板面的方向贴着P板从一端打入。①如果板间加一个垂直于纸面向外的磁场后,该带电粒子可以打出平行板区域,试求磁场的磁感应强度B的取值范围;②如果板间加一个垂直于板面从P板指向N板的电场后,带电粒子可从板间射出,则所加电场的场强怎样取值?(带电粒子的重力不计)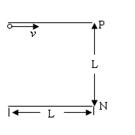
如图所示,在倾角为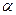 的光滑斜面上,垂直纸面放置一根长为
的光滑斜面上,垂直纸面放置一根长为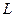 、质量为
、质量为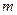 的直导体棒,当导体棒中通以垂直于纸面向里的电流
的直导体棒,当导体棒中通以垂直于纸面向里的电流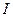 并置于竖直向上的匀强磁场中时,导体棒恰好能静止在斜面上,试求该磁场的磁感应强度是多大?如果要保持导体棒在斜面上静止且要所加磁场的磁感应强度最小,则所加磁场的方向应该怎样?最小的磁感应强度多大?
并置于竖直向上的匀强磁场中时,导体棒恰好能静止在斜面上,试求该磁场的磁感应强度是多大?如果要保持导体棒在斜面上静止且要所加磁场的磁感应强度最小,则所加磁场的方向应该怎样?最小的磁感应强度多大?
某直流电动机提升重物的装置如图所示,已知电源提供的电压 ,内阻不计,电机中的一切摩擦不计。当电机提升
,内阻不计,电机中的一切摩擦不计。当电机提升 的重物时,测得电路中的电流为
的重物时,测得电路中的电流为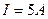 ,物体的提升速度是
,物体的提升速度是 ,
,
①试求出电机的热功率和电动机线圈的电阻R;
②若电机提拉的物体过重而无法提起,此时电机内热功率又如何?(设电机不能被烧毁)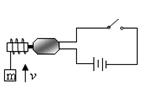
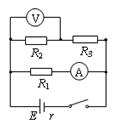
如图所示的电路中,已知电源的电动势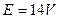 ,内阻不详,
,内阻不详,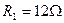 ,
,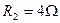 。电阻
。电阻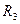 未知,将理想的安培表和伏特表接入电路中后,安培表的读数为1A,伏特表的读数为4V,试求出电源的内电阻和
未知,将理想的安培表和伏特表接入电路中后,安培表的读数为1A,伏特表的读数为4V,试求出电源的内电阻和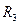 的阻值。
的阻值。