如图,四边形ABCD为矩形,AD 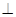 平面ABE,AE=EB=BC=2,F为CE上的点.且BF
平面ABE,AE=EB=BC=2,F为CE上的点.且BF 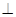 平面ACE.
平面ACE.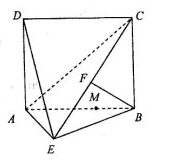
(1)求证:平面ADE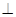 平面BCE;
平面BCE;
(2)求四棱锥E-ABCD的体积;
(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN 平面DAE.
平面DAE.
设椭圆
的左、右顶点分别为
,点
在椭圆上且异于
两点,
为坐标原点.
(Ⅰ)若直线
与
的斜率之积为
,求椭圆的离心率;
(Ⅱ)若
,证明直线
的斜率
满足
已知
是等差数列,其前
项和为
,
是等比数列,且
,
.
(Ⅰ)求数列
与
的通项公式;
(Ⅱ)记
,
,证明
(
).
如图,在四棱锥
中,
平面
.
(Ⅰ)证明
;
(Ⅱ)求二面角
的正弦值;
(Ⅲ)设
为棱
上的点,满足异面直线
与
所成的角为
,求
的长.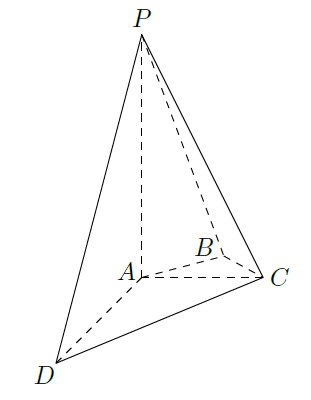
现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(Ⅲ)用
分别表示这4个人中去参加甲、乙游戏的人数,记
,求随机变量
的分布列与数学期望
.
已知函数
(Ⅰ)求函数
的最小正周期;
(Ⅱ)求函数
在区间
上的最大值和最小值.