甲、乙、丙三人进行乒乓球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判．设各局中双方获胜的概率均为
，各局比赛的结果相互独立，第1局甲当裁判．
（1）求第4局甲当裁判的概率；
（2）用X表示前4局中乙当裁判的次数，求X的分布列和数学期望．
设函数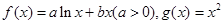 
(Ⅰ)若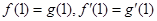
，是否存在k和m，使得 
，
，若存在，求出k和m的值，若不存在，说明理由
(Ⅱ)设 
有两个零点 
，且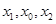 
成等差数列， 
是 G (x)的导函数，求证：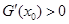 
已知椭圆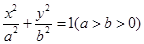 
的离心率为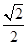 
，且过点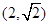 
(Ⅰ)求椭圆的标准方程；
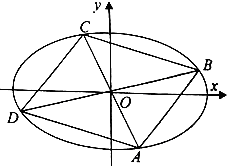
(Ⅱ)四边形ABCD的顶点在椭圆上，且对角线AC、BD过原点O，若 
．
(i)求 
的最值：
（i i）求证：四边形ABCD的面积为定值．
如图所示的几何体中，四边形ABCD是等腰梯形，AB//CD，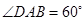 
，FC 
平面ABCD， AE BD，CB =CD=-CF．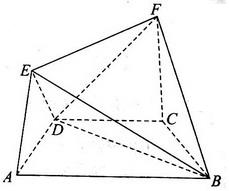
(Ⅰ)求证：平面ABCD 平面AED；
(Ⅱ)直线AF与面BDF所成角的余弦值
在乒乓球比赛中，甲与乙以“五局三胜”制进行比赛，根据以往比赛情况，甲在每一局胜乙的概率均为 
．已知比赛中，乙先赢了第一局，求：
(Ⅰ)甲在这种情况下取胜的概率；
(Ⅱ)设比赛局数为X，求X的分布列及数学期望（均用分数作答）。
在△ABC中，己知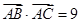 
，sinB= sinCcos
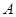，又△ABC的面积为6(Ⅰ)求△ABC的三边长；(Ⅱ)若D为BC边上的一点，且CD=1，求 
．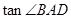